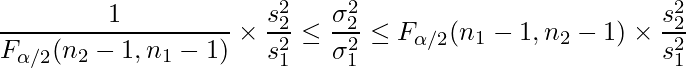- Step1. 基礎編
- 28. 等分散性の検定とWelchのt検定
28-3. 母分散の比の信頼区間の求め方
22-3章と22-4章ではカイ二乗分布を使って、母分散の信頼区間を求める方法について学びました。この章では、母分散の"比"の信頼区間の求め方について学びます。
28-1章で学んだように、確率変数が正規分布 ![]() と
と ![]() に従う2つの母集団からそれぞれサンプルサイズが
に従う2つの母集団からそれぞれサンプルサイズが ![]() 、
、![]() の標本を抽出したときの不偏分散をそれぞれ
の標本を抽出したときの不偏分散をそれぞれ ![]() 、
、![]() とします。このとき、次の式から算出される統計量Fが自由度(
とします。このとき、次の式から算出される統計量Fが自由度(![]() ,
, ![]() )のF分布に従うことを利用して母分散の比の信頼区間を算出します。
)のF分布に従うことを利用して母分散の比の信頼区間を算出します。
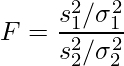
例題:
ある工場では、生産している部品AとBを1時間毎に1つ抜き取り、その重さを検査しています。計6個の部品Aの重さから算出した不偏分散は ![]() 、計11個の部品Bの重さから算出した不偏分散は
、計11個の部品Bの重さから算出した不偏分散は
![]() でした。この結果から母分散の比(b/a)の95%信頼区間を求めてみます。
でした。この結果から母分散の比(b/a)の95%信頼区間を求めてみます。
- 統計量Fを計算する
- 使用するF分布の自由度を決める
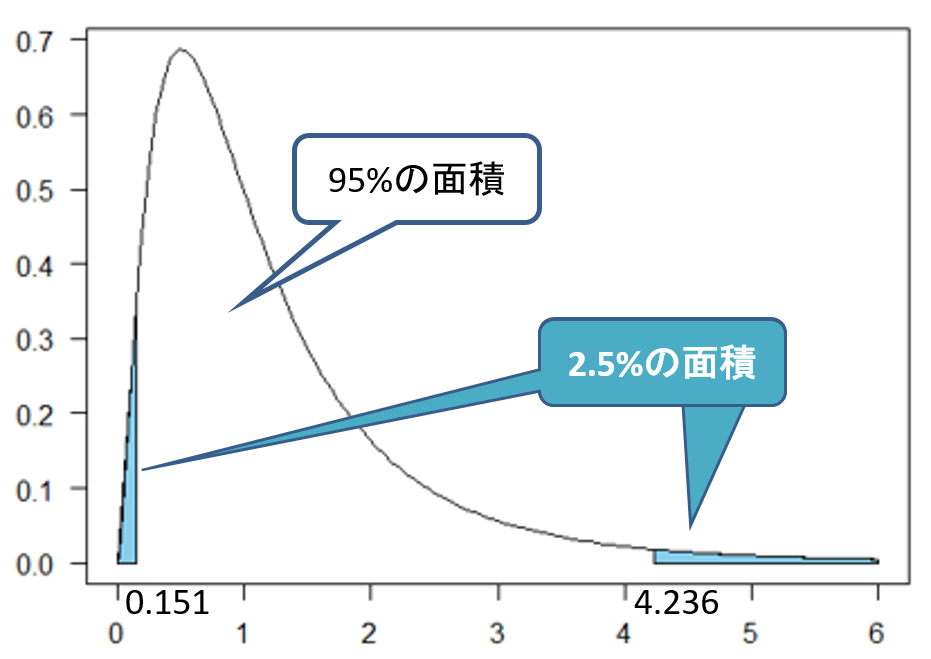
- 統計量Fの値がF分布の95%の面積(=確率)の範囲にあればいい(=両端の2.5%の面積の部分の極端な範囲に入らなければいい)ので、F分布表から自由度(5, 10)における上側2.5%点を調べる
- 95%信頼区間を求める
部品AとBの重さの不偏分散をそれぞれ ![]() 、
、![]() 、母分散をそれぞれ
、母分散をそれぞれ ![]() 、
、![]() とすると、次の式から統計量Fを求められます。
とすると、次の式から統計量Fを求められます。
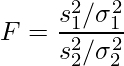
サンプルサイズは、部品Aが6、部品Bが11であることから自由度が(6-1, 11-1)=(5, 10)のF分布を用います。
※確率変数![]() が自由度(
が自由度(![]() )のF分布に従う時、その逆数である
)のF分布に従う時、その逆数である ![]() は自由度(
は自由度(![]() )のF分布に従います。したがって、自由度(
)のF分布に従います。したがって、自由度(![]() )のF分布における上側
)のF分布における上側![]() 点の値が
点の値が ![]() のとき、自由度(
のとき、自由度(![]() )のF分布における下側
)のF分布における下側![]() 点の値は
点の値は ![]() として算出できます。
として算出できます。
【F分布表 ![]() 】
】
| v2↓ v1→ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 647.789 | 799.500 | 864.163 | 899.583 | 921.848 | 937.111 | 948.217 |
| 2 | 38.506 | 39.000 | 39.165 | 39.248 | 39.298 | 39.331 | 39.355 |
| 3 | 17.443 | 16.044 | 15.439 | 15.101 | 14.885 | 14.735 | 14.624 |
| 4 | 12.218 | 10.649 | 9.979 | 9.605 | 9.364 | 9.197 | 9.074 |
| 5 | 10.007 | 8.434 | 7.764 | 7.388 | 7.146 | 6.978 | 6.853 |
| 10 | 6.937 | 5.456 | 4.826 | 4.468 | 4.236 | 4.072 | 3.950 |
| 15 | 6.200 | 4.765 | 4.153 | 3.804 | 3.576 | 3.415 | 3.293 |
統計数値表から ![]() の値を読み取ると「4.236」となっています。また、反対側の値は「
の値を読み取ると「4.236」となっています。また、反対側の値は「![]() 」の逆数を取って「
」の逆数を取って「![]() 」となります。したがって、F分布において上側2.5%点は「
」となります。したがって、F分布において上側2.5%点は「![]() 」、下側2.5%点は「
」、下側2.5%点は「![]() 」であることから、
」であることから、![]() の範囲は次のように書けます。
の範囲は次のように書けます。
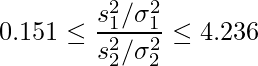
3. の式に ![]() と
と ![]() の値を代入します。
の値を代入します。
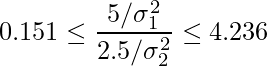
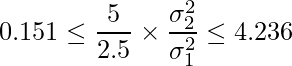
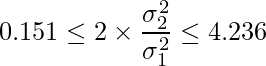
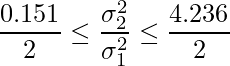
となるので、![]() の95%信頼区間を計算すると
の95%信頼区間を計算すると
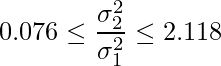
となります。
【まとめ】母分散の比の信頼区間
確率変数が正規分布 ![]() と
と ![]() に従う2つの母集団からそれぞれサンプルサイズが
に従う2つの母集団からそれぞれサンプルサイズが ![]() 、
、![]() の標本を抽出したときの不偏分散をそれぞれ
の標本を抽出したときの不偏分散をそれぞれ![]() 、
、![]() とすると、次の式から母分散の比
とすると、次の式から母分散の比 ![]() の
の ![]() 信頼区間を求めることができる。ただし、「
信頼区間を求めることができる。ただし、「![]() 」は自由度が
」は自由度が ![]() のF分布における上側確率が
のF分布における上側確率が ![]() となる値を、「
となる値を、「![]() 」は下側確率が
」は下側確率が ![]() となる値を示す。
となる値を示す。
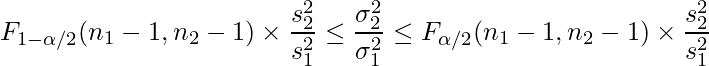
ただし、この式は次の式と同義である。