- Step1. 基礎編
- 23. 検定の前に
23-4. 第1種の過誤と第2種の過誤
23-3章で学んだ第1種の過誤と第2種の過誤を表にまとめると次のようになります。
| 真実 | |||
| 帰無仮説が正しい | 対立仮説が正しい | ||
| 検定の結果 | 帰無仮説を棄却しない (対立仮説が正しいとは言えない) | 正しい | 第2種の過誤( |
| 帰無仮説を棄却する (対立仮説が正しい) | 第1種の過誤( | 正しい( | |
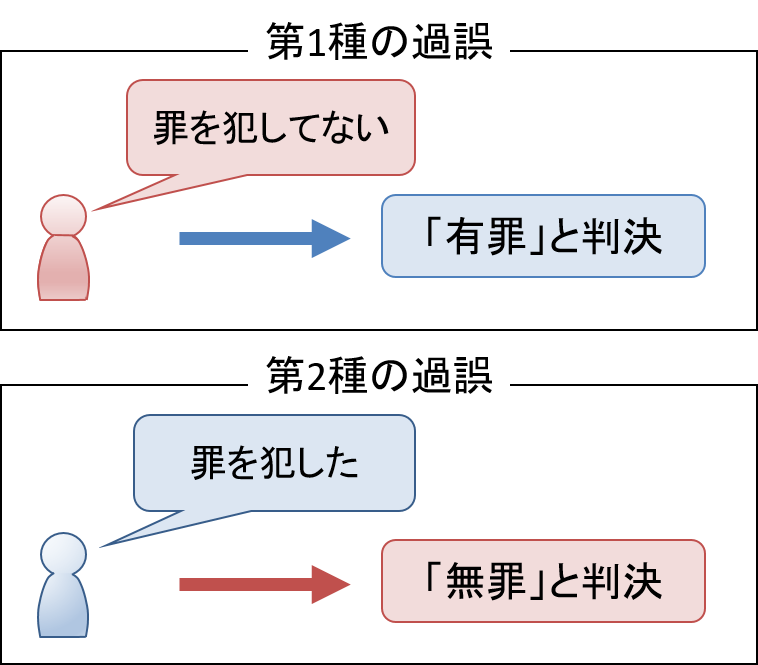
ある罪を犯した容疑者の裁判を例に取ってみます。帰無仮説![]() を「この容疑者は無罪である」とします。このとき、本当はこの容疑者は無罪なのに有罪という判決を受ける(本当は帰無仮説
を「この容疑者は無罪である」とします。このとき、本当はこの容疑者は無罪なのに有罪という判決を受ける(本当は帰無仮説![]() が正しいのに帰無仮説
が正しいのに帰無仮説![]() が棄却され、対立仮説
が棄却され、対立仮説![]() が採択されてしまう)確率が第1種の過誤の確率です。一方、本当はこの容疑者は有罪なのに無罪という判決を受ける(本当は対立仮説が正しいのに帰無仮説
が採択されてしまう)確率が第1種の過誤の確率です。一方、本当はこの容疑者は有罪なのに無罪という判決を受ける(本当は対立仮説が正しいのに帰無仮説![]() が棄却されない)確率が第2種の過誤の確率です。
が棄却されない)確率が第2種の過誤の確率です。
| 真実 | |||
| 本当は無罪 (帰無仮説が正しい) | 本当は有罪 (対立仮説が正しい) | ||
| 裁判の結果 | 無罪と判決 (対立仮説が正しいとは言えない) | 正しい | 第2種の過誤( |
| 有罪と判決 (対立仮説が正しい) | 第1種の過誤( | 正しい( | |
第1種の過誤の確率(![]() )も、第2種の過誤の確率(
)も、第2種の過誤の確率(![]() )も共に低いほうがよいことは想像がつきます。しかしながら、両方はトレード・オフの関係になっているので同時に低くすることはできません。
)も共に低いほうがよいことは想像がつきます。しかしながら、両方はトレード・オフの関係になっているので同時に低くすることはできません。
ある容疑者の裁判の例では、第1種の過誤を犯す確率を下げるために容疑者を全て無罪にしてしまうと、有罪の人まで無罪になってしまうために第2種の過誤を犯す確率が上がってしまいます。逆に第2種の過誤を犯す確率を下げるために容疑者を全て有罪にしてしまうと、本来無罪の人まで有罪になってしまうために第1種の過誤を犯す確率が上がってしまいます。したがって、第1種の過誤を犯す確率と第2種の過誤を犯す確率のバランスをとることが重要です。
【コラム】第1種の過誤、第2種の過誤の様々な例
■防犯システムの場合
帰無仮説![]() を「泥棒が侵入したと判定され、防犯システムが作動する」とします。このとき第1種の過誤と第2種の過誤は次のようになります。
を「泥棒が侵入したと判定され、防犯システムが作動する」とします。このとき第1種の過誤と第2種の過誤は次のようになります。
- 第1種の過誤:本当は泥棒が侵入したのに泥棒が侵入したと判定されず、防犯システムが作動しない
- 第2種の過誤:本当は泥棒が侵入していないのに泥棒が侵入したと判定され、防犯システムが作動する
■新しい薬の効果の場合
帰無仮説![]() を「新しい薬は古い薬と同じくらいの効果がある」とします。このとき第1種の過誤と第2種の過誤は次のようになります。
を「新しい薬は古い薬と同じくらいの効果がある」とします。このとき第1種の過誤と第2種の過誤は次のようになります。
- 第1種の過誤:本当は新しい薬は古い薬と同じくらいの効果があるのに、同じくらいの効果はないと結論付けられる
- 第2種の過誤:本当は新しい薬は古い薬と同じくらいの効果はないのに、同じくらいの効果があると結論付けられる
23. 検定の前に
事前に読むと理解が深まる- 学習内容が難しかった方に -
- ブログ
よくある間違い
- ブログ
p値と有意水準
- ブログ
P = 0.05 だったら