答えを見る

答え閉じる

統計的仮説検定を行う場合、まず（①　帰無）仮説を設定します。次に、データから統計量を算出します。その統計量より極端な値をとる確率が（②　P値）です。（②　P値）から結論を導くために、（③　有意水準）を設定します。（③　有意水準）は検定を行う前に設定しておかなくてはなりません。

（②　P値）が（③　有意水準）より小さくなった場合、（④　帰無）仮説を棄却します。このとき（⑤　対立）仮説が正しいと結論づけられます。一方、逆の場合は（⑥　帰無）仮説が正しいということはできません。これは検定が（⑦　背理）法を用いているためです。

答えを見る

答え閉じる

1. ×：第2種の過誤の確率を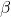とすると検出力はで計算します。
2. ◯：正しいです。
3. ×：検出力が低いほど、本当は有意な結果であるにも関わらず、有意性を正しく検出できない確率が高くなります。
4. ×：サンプルサイズと検出力は密接に関係しており、サンプルサイズが大きいほど検出力も高くなる傾向にあります。

答えを見る

答え閉じる

有意ではありません。

検定は、事前に設定した有意水準と比較し結論を出します。このとき、p値が有意水準より低ければ検定は有意となります。逆に、有意水準より高い場合は有意にはなりません。

答えを見る

答え閉じる

1. ×：誤りです。検定は、事前に設定した有意水準と比較して結果を決めます。p値がどんなに低くても、有意水準より高ければ有意とはなりません。
2. ×：設定した帰無仮説に応じて片側か両側かを選択します。有意になるかならないかで決めるのは正しくありません。
3. ×：誤りです。有意水準は、検定を行う前に定める必要があります。恣意的に結果を変えられるような方法を取るのは間違いです。
4. ×：誤りです。p値は、「帰無仮説が正しい場合に、それよりも極端なデータが観測される確率」です。仮説について何か直接的な確率を計算するものではありません。
5. ×：誤りです。検定が有意ではない場合、帰無仮説が正しいのではなく「帰無仮説を棄却できない」という解釈となります。この場合だと、「男性の平均体重が60kgでないとは言えない。」という結論となります。

答えを見る

答え閉じる

1. ：第一種の過誤が起こった場合、本当は帰無仮説が正しいのに誤って帰無仮説を棄却してしまっています。つまり、「体重を減少させる効果がない」のに「体重を減少させる効果がある」という結論を下していることになります。残念ながら、健康法には効果はなく体重が減少しないでしょう。
2. ：検定が正しかった場合、この健康法には体重を減少させる効果があると考えられます。しかしながら、具体的にどれくらいの効果があるかを教えてはくれません。ものすごく体重が減るかもしれませんし、数十g程しか体重が減らないかもしれません。

統計的仮説検定では、効果や差の有無を検証することは可能ですが、その大きさについて具体的に知ることはできない点に注意が必要です。