24-1. 母平均の検定（両側t検定）

検定は次の流れに従って行います。

例題：

ある工場では部品Aを製造しています。製造された部品Aの中からランダムに10個を選び長さを測定したところ、平均値は7.2cm、不偏分散は0.04 $cm^2$ でした。部品Aの長さが正規分布に従うとき、この工場で製造している部品Aの長さは7.0cmといえるでしょうか。

帰無仮説 $H_{0}$ は「部品Aの長さは7.0cmである」とします。したがって、対立仮説 $H_{1}$ は「部品Aの長さは7.0cmではない」となります。

ここでは有意水準 $\alpha$ ＝0.05とします。

この実験では母分散が分からないので、不偏分散 $s^{2}$ を用いる統計量tを使います。統計量tは次の式から求められます。 $\overline{x}$ はデータの平均、 $\mu$ は母平均、 $n$ はサンプルサイズを表します。

$\displaystyle t=\frac{\overline{x}-\mu}{\sqrt{\frac{s^{2}}{n}}}$

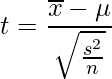
この検定で使用する分布は自由度「10-1=9」の「t分布」です。また、この工場で製造する部品Aの長さが7.0cmであるかどうかを調べることが目的なので、両側検定を行います。統計数値表から $t_{0.025}(9)$ の値を読み取ると「2.262」となっています。

$\displaystyle t=\frac{7.2-7.0}{\sqrt{\frac{0.04}{10}}}=\frac{7.2-7.0}{\frac{0.2}{\sqrt{10}}} \fallingdotseq 3.16$

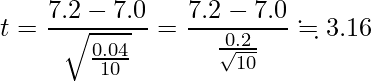
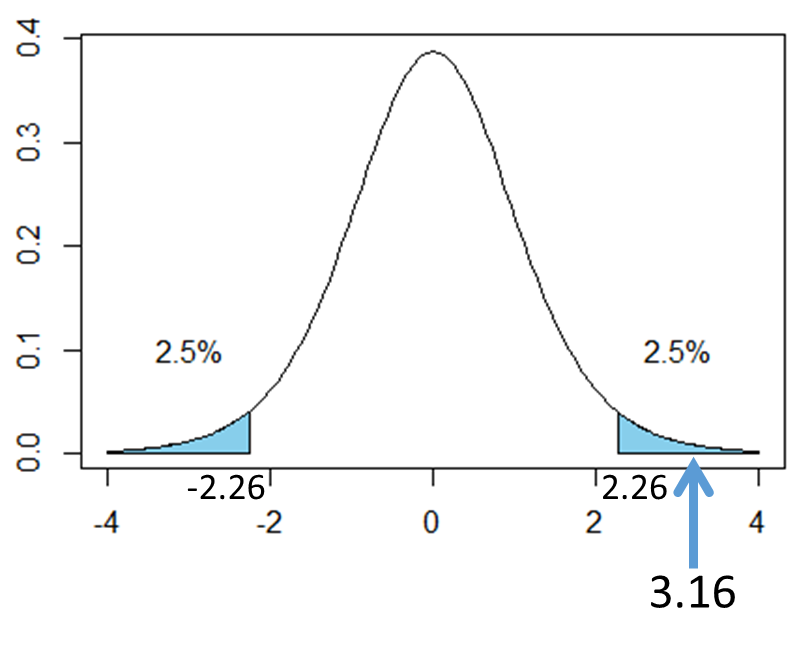
次の図は、自由度9のt分布を表したものです。t=3.16は、図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において、帰無仮説を棄却し、対立仮説を採択する」という結果になります。つまり、「この工場で製造している部品Aの長さは7.0cmではない」と結論づけられます。

勉強の合間にどうぞ。説明がとてもとても丁寧です。

created by Rinker

光文社

¥858 (2024/10/30 16:17:13時点 Amazon調べ-詳細)