- 24. 平均値の検定
練習問題(24. 平均値の検定)
以下の問題でt分布表が必要な場合、ページ下部の表を用いてよい。
1
一般に、ビールの大瓶の容量は633mlであると言われている。あるメーカーのビール大瓶をサンプリングし、その平均が633mlよりも少ないかどうか検定したい。この場合、帰無仮説と対立仮説をどのように設定するのが適切であるか答えよ。

答えを見る
- 答え
 閉じる
閉じる -
帰無仮説は、「ビールの容量は633mlである」となります。一方で、対立仮説は「ビールの容量は633mlではない」と設定するのではなく、「ビールの容量は633mlよりも少ない」となります。これは確かめたい仮説が、「633mlよりも少ないかどうか」であり、633mlより多い場合については考慮する必要はないためです。
2
あるメーカーのビール大瓶10本をサンプリングし、その平均が633mlよりも少ないかどうか検定したい。測定したビール10本の容量が次の表の通りである場合、検定の結果はどのようになるか答えよ。なお、有意水準は![]() とし、ビール大瓶の容量は正規分布に従うものとする。
とし、ビール大瓶の容量は正規分布に従うものとする。
| No. | 容量[ml] |
|---|---|
| 1 | 632.9 |
| 2 | 633.1 |
| 3 | 633.2 |
| 4 | 632.3 |
| 5 | 633.1 |
| 6 | 634.7 |
| 7 | 633.6 |
| 8 | 633.0 |
| 9 | 632.4 |
| 10 | 633.6 |

答えを見る
- 答え
 閉じる
閉じる -
この問題では、帰無仮説を「容量は633mlである」、対立仮説を「容量は633mlよりも少ない」として片側検定を行います。10本のビールの容量の平均を計算すると633.19mlとなり、633mlよりも多くなります。
「容量は633mlよりも少ないかどうか」のような方向性のある仮説を検証するための片側検定では、平均値が633mlより大きくなってしまった時点で検定を終了し「帰無仮説を棄却できない=633mlより少ないとは言えない」と結論付けます。
同様に対立仮説を「容量は633mlよりも大きい」と設定した片側検定では、標本の平均が633mlを下回った時点で検定を終了します。
3
次の表は、1つ25.5 kgの強力粉20個をサンプリングし、重量を測定した結果をまとめたものである。このデータを用いて、強力粉の重量は25.5 kgではないと言えるかどうか検定せよ。なお、有意水準は![]() とし、強力粉の重量は正規分布に従うものとする。
とし、強力粉の重量は正規分布に従うものとする。
| 項目 | 測定結果 |
|---|---|
| サンプルサイズ | 20 |
| 平均 | 25.29 |
| 不偏分散 | 2.23 (= |

答えを見る
- 答え
 閉じる
閉じる -
この問題では、帰無仮説を「平均重量は25.5kgである」、対立仮説を「平均重量は25.5kgではない」として両側t検定を行います。統計量tは次の式から計算できます。
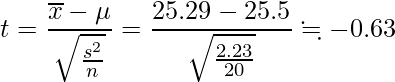
自由度19のt分布の両側5%点は、-2.093または2.093です。したがって、
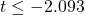 または
または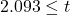 が棄却域となりますが、
が棄却域となりますが、 であるため、帰無仮説を棄却できません。以上の事から「平均重量は25.5kgでないとは言えない」と結論付けられます。
であるため、帰無仮説を棄却できません。以上の事から「平均重量は25.5kgでないとは言えない」と結論付けられます。
4
ある島には非常に珍しい鳥が生息している。研究員がその鳥の数(羽)を1年間に10回調査したところ、平均25、不偏分散9(=![]() )であった。この結果から、この島には21を超える数の鳥が生息していると言えるかどうか検定せよ。なお、有意水準は
)であった。この結果から、この島には21を超える数の鳥が生息していると言えるかどうか検定せよ。なお、有意水準は![]() とし、調査によって観察される鳥の数は正規分布に従うものとする。
とし、調査によって観察される鳥の数は正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
この問題では、帰無仮説を「生息数は平均21である」、対立仮説を「生息数は平均21を超える」として片側t検定を行います。統計量tは次の式から計算できます。
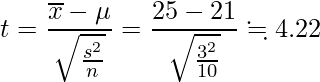
自由度9のt分布の片側5%点は、1.833です。したがって、
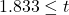 が棄却域となりますが、
が棄却域となりますが、 であるため、帰無仮説を棄却します。以上の事から「生息数は平均21を超える」と結論付けられます。
であるため、帰無仮説を棄却します。以上の事から「生息数は平均21を超える」と結論付けられます。
5
あるパンメーカーでは、人気の商品であるメロンパンを2つの工場で製造している。2つの工場で製造されているメロンパンの重量(g)を調べた結果、A工場の10個については平均93、不偏分散![]() であった。また、B工場の8個については平均87、不偏分散
であった。また、B工場の8個については平均87、不偏分散![]() であった。この2工場の間でメロンパンの重量(g)に差があると言えるかどうか検定せよ。なお、有意水準は
であった。この2工場の間でメロンパンの重量(g)に差があると言えるかどうか検定せよ。なお、有意水準は![]() とし、それぞれの工場で製造されるメロンパンの重量はそれぞれ正規分布に従い、かつ、分散は等しいものとする。
とし、それぞれの工場で製造されるメロンパンの重量はそれぞれ正規分布に従い、かつ、分散は等しいものとする。

答えを見る
- 答え
 閉じる
閉じる -
この問題では、帰無仮説を「2つの工場の間でメロンパンの重量に差はない」、対立仮説を「2つの工場の間でメロンパンの重量に差がある」として両側t検定をいます。まず2つの標本をプールした分散を算出します。
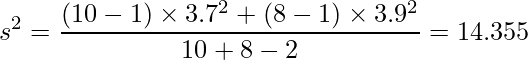
この値を統計量tの式に代入すると次のようになります。
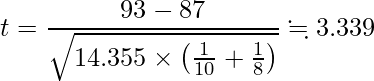
自由度16のt分布の両側5%点は、2.120です。したがって、
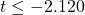 または
または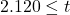 が棄却域となりますが、
が棄却域となりますが、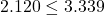 であるため、帰無仮説を棄却します。以上の事から「2つの工場の間でメロンパンの重量に差がある」と結論付けられます。
であるため、帰無仮説を棄却します。以上の事から「2つの工場の間でメロンパンの重量に差がある」と結論付けられます。
t分布表
| α | |||||
|---|---|---|---|---|---|
| v | 0.1 | 0.05 | 0.025 | 0.01 | 0.005 |
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 |
| 3 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 |
| 4 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 6 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 |
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 |
| 8 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 |
| 9 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 11 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 |
| 12 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 |
| 13 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 |
| 14 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 |
| 15 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 |
| 16 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 |
| 17 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 |
| 18 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 |
| 19 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 |






