Step1. 基礎編
24. 平均値の検定

24-2. 母平均の検定（片側t検定）

例題：

あるメーカーの電球は、寿命が2,000時間であると宣伝しています。このスペックが本当であるかを確かめるため、この電球を様々なお店で合計15個購入しテストを行ったところ、寿命の平均値は1,900時間、不偏分散は $150^2$ 時間でした。この電球の寿命が正規分布に従うとき、この結果からこの電球の宣伝文句は問題ないと考えられるでしょうか。

仮説を立てる

帰無仮説 $H_{0}$ は「この電球の寿命は2,000時間である」とします。また、電球の寿命が2,000時間よりも長い場合は特に問題はなく、2,000時間より短いかどうかのみを考えればよいので、対立仮説 $H_{1}$ を「この電球の寿命は2,000時間よりも短い」とします。

有意水準を設定する

$\alpha$ ＝0.05とします。

適切な検定統計量を決める

この実験では母分散が分からないので、統計量zではなく不偏分散 $s^{2}$ を用いる統計量tを使います。統計量tは次の式から求められます。 $\overline{x}$ はデータの平均、 $\mu$ は母平均、 $n$ はサンプルサイズを表します。

$\displaystyle t=\frac{\overline{x}-\mu}{\sqrt{\frac{s^{2}}{n}}}$

棄却ルールを決める

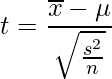
この検定で使用する分布は自由度「15-1=14」の「t分布」です。また、電球の寿命が2,000時間よりも長い場合は特に問題はなく、2,000時間より短いかどうかのみを考えればよいので、片側検定を行います。統計数値表から $t_{0.05}(14)$ の値を読み取ると「1.761」となっています。

検定統計量を元に結論を出す

$\displaystyle t=\frac{1900-2000}{\sqrt{\frac{150^2}{15}}}=\frac{1900-2000}{\frac{150}{\sqrt{15}}} \fallingdotseq -2.58$

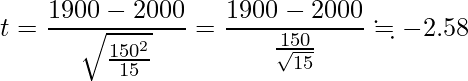
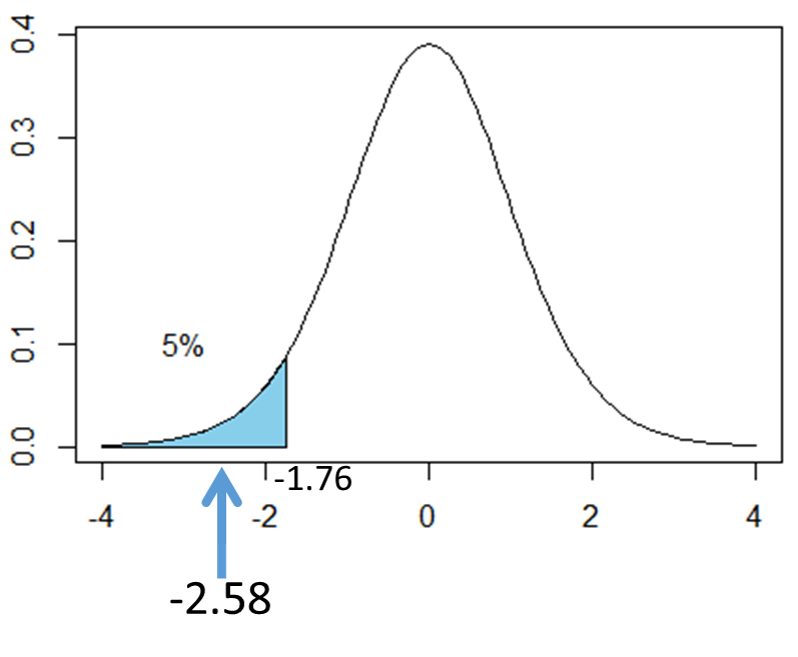
次の図は自由度14のt分布を表したものです。t=-2.58は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%において、帰無仮説は棄却され、対立仮説が採択される」という結果になります。つまり、「この電球の寿命は2,000時間より短いので、宣伝文句は修正した方がいい」と結論づけられます。