- Step1. 基礎編
- 24. 平均値の検定
24-3. 2標本t検定とは
2つの独立した母集団があり、それぞれの母集団から抽出した標本の平均に差があるかどうかを検定することを「2標本t検定」といいます。例えば、ある学校で行ったテストの点数が1組と2組とで差があるかどうかの検定や、被験者に対してある薬を投与する前後で血圧がどう変化したかの検定に使います。ただし、2つのデータが「対応のあるデータ」か「対応のないデータ」かによって検定統計量の算出方法が異なります。
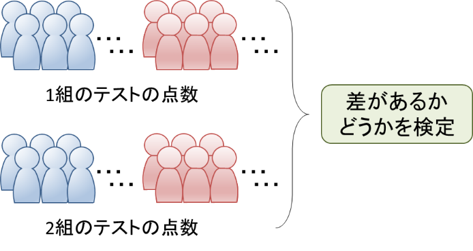
■対応がない場合の2標本t検定の方法
異なる対象から抽出された2つの標本は「対応のないデータ(対応なし)」です。 例えば、1組と2組の生徒は異なるので、それぞれのクラスから抽出された2つの標本は「対応のないデータ」となります。
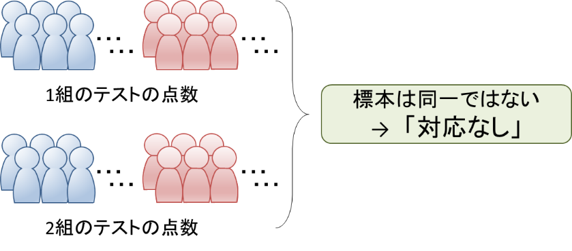
対応がない場合の2標本t検定では、2つの標本に対応がないことを加味した検定統計量を用いる必要があります。20-6章で学んだように、母分散が分からない場合、1群目の標本平均を![]() 、母平均を
、母平均を![]() 、サンプルサイズを
、サンプルサイズを![]() 、2群目の標本平均を
、2群目の標本平均を![]() 、母平均を
、母平均を![]() 、サンプルサイズを
、サンプルサイズを![]() としたときに、次の式から算出される統計量tを使います。検定で用いるのは自由度
としたときに、次の式から算出される統計量tを使います。検定で用いるのは自由度![]() のt分布です。
のt分布です。
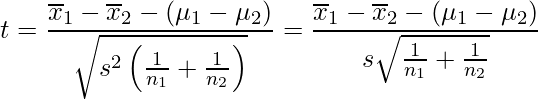
ただし、帰無仮説である「母平均が等しい」という仮説が正しいとすると、![]() になります。したがって、
になります。したがって、
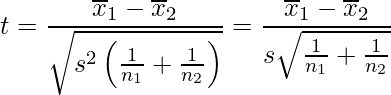
となります。この式には2つの標本の不偏分散を用いて算出した「プールした分散![]() 」を使っています。プールした分散とは、2つの標本の不偏分散を1つにまとめたもので、1群目の不偏分散を
」を使っています。プールした分散とは、2つの標本の不偏分散を1つにまとめたもので、1群目の不偏分散を![]() 、2群目の不偏分散を
、2群目の不偏分散を![]() とした場合、下の式から求めることができます。2つの標本のデータを1つにまとめることで、分散の推定精度を高めることができます。
とした場合、下の式から求めることができます。2つの標本のデータを1つにまとめることで、分散の推定精度を高めることができます。
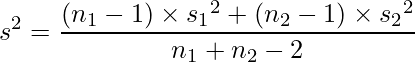
■対応がある場合の2標本t検定の方法
一方、同一の対象から抽出された「対」となる2つの標本は「対応のあるデータ(対応あり)」です。例えば、数人の被験者に対して投薬実験を行った場合に、投薬前後で得られる同一被験者由来の対となる標本は「対応のあるデータ」となります。
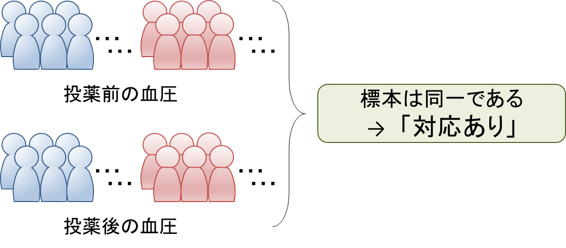
対応がある場合の2標本t検定では、「対応のあるデータの差」を用いて検定を行います。差を用いると実質は1標本の検定となるので、「24-1. 母平均の検定(両側t検定)」や「24-2. 母平均の検定(片側t検定)」と同様のやり方で行います。帰無仮説![]() は「対応のあるデータの差の平均は0である」となります。
は「対応のあるデータの差の平均は0である」となります。
■おすすめ書籍
満を持して登場の通称”赤本”です。統計検定®2級対策本として様々なところで紹介されているのを目にしたことがある方も多いかもしれません。統計学基礎の内容がしっかりまとまっている1冊である反面、やや難しいです。初学者の方が一番初めに手に取る本としてはあまりおすすめできませんが、勉強を進めていくと理解できるページが増えてきて、統計の知識が盤石なものになっていくのではないかと思います。
24. 平均値の検定
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 20. 母平均の区間推定(母分散未知)
20-6. 母平均の差の信頼区間
- ブログ
対応のあるデータの検定(1)
- ブログ
対応のあるデータの検定(2)
- ブログ
平均値の差の検定








