対応のあるデータの検定(2)─マクネマー検定

2017/08/14

※コラム「統計備忘録」の記事一覧はこちら※

前回は、対応のあるデータの「ｔ検定」の例として、閉眼片足立ちの時間に対するバランスボールのトレーニング効果を取り上げました。バランスボールは、バランス能力を鍛えるだけでなく、ストレッチやダイエット、腰痛改善など幾つかの効果が期待されています。今回は、腰痛改善効果を検定する方法を考えてみましょう。

腰痛は、閉眼片足立ちの時間ように数値にして状態を把握することが困難です。そこで今回は、腰痛の「ある」、「なし」を自己評価してもらうことにします。実験参加者は、100人のオフィスワーカー。1ヶ月間、毎日1時間、バランスボールに指示された通りに座ってもらいます。

実験の結果をクロス集計表にまとめると、次のようになりました。

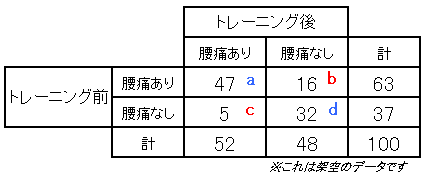
クロス集計表から検定するとなると、独立性の検定を思い浮かべるかもしれませんが、今回は、マクネマー検定という方法を用います。計算に用いるのは、前後で状態が変化した人達、「(b)腰痛あり→腰痛なし」と「(c)腰痛なし→腰痛あり」の人数です。

bとcが同数であれば改善効果無し、b＞cなら改善効果あり、b＜cなら逆効果ということになります。検定統計量（c²）は次の式で求めます。c²は自由度1のカイ二乗分布に従います。

＜前提＞
　帰無仮説：「トレーニング効果は無い（b=c）」
　対立仮説：「トレーニング効果がある（bとcは異なる）」
　有意水準α=0.05
＜計算＞
　c²=(|b-c|-1)²/(b+c)=(|5-16|-1)²/(5+16)= 4.762

c²≧4.762の上側累積確率は「0.029」となり、腰痛の改善効果はありそうです。独立性の検定では「a x d」と「b x c」の差が重要で、「bとc」の差は有意性とは関係無かったのに対し、マクネマー検定では「bとc」に差が無ければ有意にならないという点に留意してください。

対応のあるデータの検定には、3群以上に対応したもの、ノンパラメトリック法によるものなど、他にも幾つか検定手法があります。エクセル統計では次のメニューから対応のあるデータの検定を行うことができます。