対応のあるデータの検定(1)
2017/08/14
カテゴリ:コラム「統計備忘録」
タグ:統計備忘録
※コラム「統計備忘録」の記事一覧はこちら※
同じ人から条件を変えて複数回のデータをとるケースがあります。例えば、バランスボールでトレーニングする前と後の閉眼片足立ちの時間。降圧剤を飲んだ人の直後と2時間後、4時間後の血圧。選挙の前後の支持政党。このようにして得られたデータを「対応のある(一対の、paired)」、あるいは、「反復測定(重複測定、repeated measurement)による」データと言います。
対応のあるデータの場合、検定の対象となるのは状態の変化です。次の例を見てください。
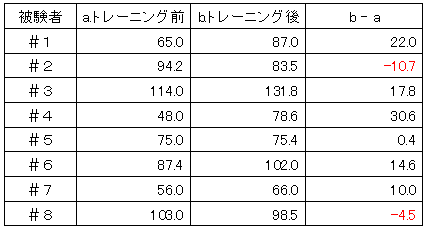 ※これは架空のデータです
※これは架空のデータです
このデータはバランスボールによる1週間のトレーニングを行う前(a)と、行った後(b)の閉眼片足立ちの時間(秒)です。バランスボールは、腰掛けているだけでも体の左右の筋肉バランスを整えてくれるので、閉眼片足立ちにはもってこいのトレーニングです。8人中6人にトレーニングの効果(b-a)が現れています。8人を平均すると10秒記録が伸びています。これをグラフにすると次のようになります。
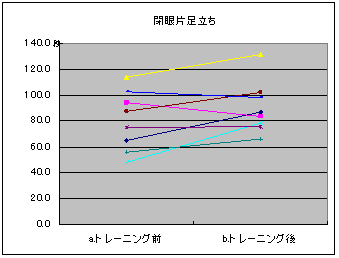
バランスボールによるトレーニング効果があった人は、前後を結ぶ線が右上がりに、効果が無ければ線は水平から右下がりになります。このように、線の傾き具合から変化の度合いを読み取ることができます。トレーニング効果による変化だけに注目したのが次のグラフです。
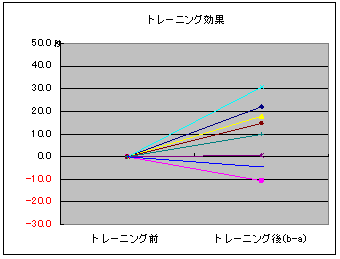
このグラフにすると、よりトレーニング効果が鮮明になります。この変化の度合いを検定する方法が「対応のあるスチューデントのt検定」です。計算の対象となるのはトレーニング効果(b-a)だけです。トレーニング効果の平均値と標準誤差
(標準偏差/√データの個数)を求めさえすればt値が求まります。
<前提>
帰無仮説:「トレーニング効果の母平均値はゼロである」
対立仮説:「トレーニング効果はある(効果の母平均値はゼロより大きい)」
有意水準α=0.05の片側検定
<計算>
t=平均値/標準誤差 = 10.025/4.966=2.018
v=計算に使ったデータの個数-1=8-1=7
私はバランスボールの効果で記録が伸びると信じていましたので、片側検定の結果を採用します。自由度が7のt分布で、t≧2.018の上側累積確率は「0.042」となり、私の仮説は支持されました。
対応のあるデータでは、有意になりやすいかどうかは、変化の量よりも、変化の向きがポイントになります。変化量が小さくとも、向きが揃っていれば有意になりやすい性質があります。グラフにした場合、次のように線と線がクロスすることなく、どの線も似たような傾きになっていれば(ほぼ並行になっていれば)、傾きが僅かでも、まず検定結果は有意になるでしょう。
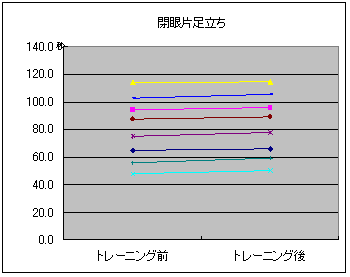
逆に、有意にならないケースは、次のように線がクロスする頻度の高いときです。
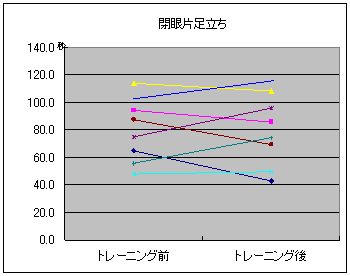
このように対応のあるデータを分析するときは、対応のあるデータ同士を線で結んだ折れ線グラフを作ると、検定結果を容易に予測することができます。







