※コラム「統計備忘録」の記事一覧はこちら※

2群の平均値の差をt検定する手法は幾つかあります。エクセル統計のユーザーなら次の3つを覚えておいて損はありません。

1. スチューデントのt検定
2. 分散分析
3. 回帰分析

手法選択のポイントは、Excel のワークーシートにどのようにデータを入力したかによります。

パターン(1)

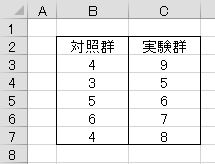
このように群単位にデータを1列ずつにまとめたなら、エクセル統計のメニューから次の2つのどちらかを選択します。

• ［2標本の比較］−［母平均の差の検定（表形式）］
• ［分散分析・多重比較］−［一元配置分散分析］

前者ならスチューデントのt検定、

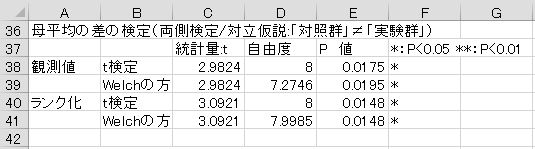
後者なら一元配置分散分析の結果が得られます。

統計のテキストには「3群以上の検定のときには分散分析を使う」と書いてあることが多いようですが、2群の場合でも分散分析を使うことに問題はありません。

t検定の両側p値と、分散分析表の因子Aのp値は、どちらも「0.0175」と同じ値になります。t値を知りたいのなら、Excel のSQRT関数でF値の二乗根を求めます。
　=SQRT(8.8947)

パターン(2)

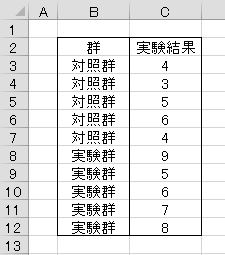
このように「対照群」、「実験群」と群の区別を個々に記録したのなら、エクセル統計のメニューから、［2標本の比較］−［母平均の差の検定（データベース形式）］を選択します。

ダイアログ上の、検定を行う変数に「実験結果」を、標本を識別する変数に「群」を設定します。

パターン(3)

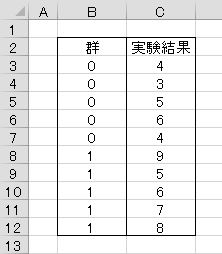
前のパターン(2)から、「対照群」を「0」に、「実験群」を「1」にと、群の区別を数値に置き換えることで回帰分析が使えます。回帰分析では群の区別が説明変数（独立変数）、実験結果が目的変数です。

分析を行うには、エクセル統計のメニューから、［多変量解析］−［重回帰分析］を選択します。結果は次の通りです。

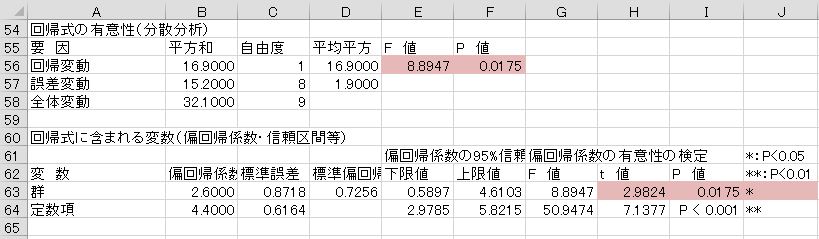
重回帰式の出力の中で、群の偏回帰係数「2.6」は対照群と実験群の平均値の差になります。その右側の赤網掛けの箇所は、「偏回帰係数はゼロである」という仮説を検定した結果で、有意水準5％未満で仮説が棄却されたので、「偏回帰係数（＝2群の平均値の差）はゼロではない」ということになり、p値は「0.0175」でスチューデントのt検定と全く同じ結論が導かれます。

右下の分散分析表は、回帰分析から得られた次の重回帰式により、実験結果のデータ変動を説明できているかどうか、検定した結果です。

　実験結果（y）＝4.4＋2.6×群（x）

内容は一元配置分散分析をしたときと全く同じです。要因の表記が「群」から「回帰変動」に変わっただけです。

この他に「無相関の検定」で代用することも可能です。どれを使っても同じ結論が得られることから、手法に合わせてデータを変形するよりも、Excel に入力済みのデータに合わせて、最も手間の少ない手法を選択すれば良いのです。