重回帰分析 : Multiple Regression Analysis
概要
重回帰分析とは、説明変数(独立変数)と1個の目的変数(従属変数)の間に直線の式をあてはめ、目的変数の変動が説明変数の変動によってどの程度影響されるかを分析する手法です。あてはめる式を重回帰式とよび、最小二乗法により求めます。p個の変数がある場合の重回帰式は以下の式で表されます。
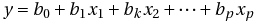
b1, b2, …, bpは偏回帰係数といい、各説明変数が1単位変動する毎に目的変数に与える影響を示します。b0は定数項を、x1, x2, …, xpは説明変数を、yは目的変数を表します。重回帰式の検定は分散分析によって行います。
変数選択
本製品は、変数選択の方法として「変数増減法」、「変数減増法」、「変数増加法」、「変数減少法」の4種類を搭載しています。変数選択の機能を用いることで、目的変数との相関関係が強い説明変数を自動的に選択することができます。
多重共線性
説明変数間に強い相関があると多重共線性という現象が発生し、偏回帰係数の解釈が難しくなります。VIFではVIF > 10の場合、トレランスではトレランス < 0.1の場合に多重共線性が疑われます(cf. トレランス = 1/VIF)。また、これらの基準を満たさない場合でもVIFが高い場合や、トレランスが小さい場合も注意が必要です。多重共線性が見受けられる場合、相関の強い変数のいずれか一方を除いて再度分析を行うことをお勧めします。
分析例ファイルのダウンロード
重回帰分析を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
データベース形式
| データサイズ範囲 | 処理対象データ | ||||
|---|---|---|---|---|---|
| 行数 | 列数 | 数値 | 文字列 | 空白 | |
| 目的変数 | 3~60,000行 | 1列 | ○ | 欠 | 欠 |
| 説明変数 | 3~60,000行 | 1~100列 | ○ | 欠 | 欠 |
| 度数※1 | 3~60,000行 | 1列 | ○ | 欠 | 欠 |
※:○…処理可、×…処理不可、欠…欠損値として除く
※1:度数の和(データ件数の合計)が60,000 以下であること
設定項目
Excelの[エクセル統計]タブから、[多変量解析]→[重回帰分析]を選択すると以下のダイアログが表示されます。
「変数」タブ

- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力範囲のダイアログが表示されるので、データ入力範囲を設定して [戻る] ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- 目的変数 必須
- [変数リスト]から目的変数とする変数を設定します。
- 説明変数 必須
- [変数リスト] から説明変数とする変数を設定します。
- 度数
- [変数リスト]から度数に用いる変数を設定します。
目的変数と説明変数のいずれかに「空白」や「文字」が入力されているケースは分析対象から除かれ、目的変数と説明変数が全て揃っているケースが分析対象となります。ただし、説明変数がすべて入力されていれば予測値の計算は行います。
「変数選択」タブ
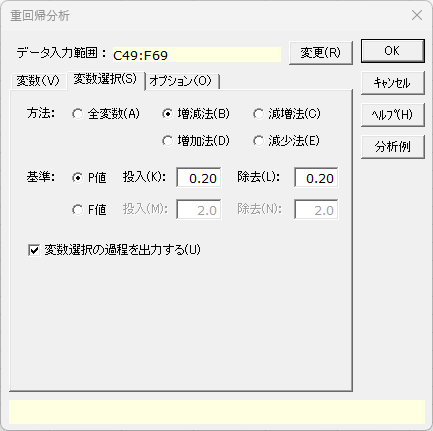
- 方法 必須
- [全変数]、[増減法]、[減増法]、[増加法]、[減少法]の5つから選択します。初期設定は[全変数]です。
- 基準
- 変数選択を行う場合、変数選択の基準として [P値] と [F値] のいずれかを選択します。[増減法]、[減増法]、[増加法] のいずれかを選択した場合、変数投入の基準値を[投入] テキストボックスに指定します。[増減法]、[減増法]、[減少法]のいずれかを選択した場合、変数除去の基準値を [除去] テキストボックスに指定します。P値は0.0001以上0.9999以下の値を、F値は0.00001以上99999以下の値を入力してください。
- 変数選択の過程を出力する
- 変数選択の過程を出力する場合、このチェックボックスをオンにします。初期設定はオフです。
「オプション」タブ
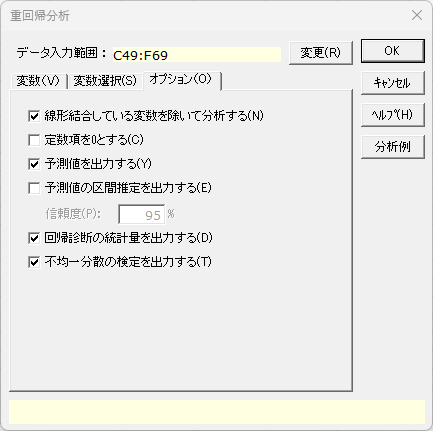
- 線形結合している変数を除いて分析する
- 線形結合している変数を最初に除いてから分析する場合、このチェックボックスをオンにします。初期設定はオンです。
- 定数項を0とする
- 定数項を0として重回帰式の推定を行う場合、このチェックボックスをオンにします。初期設定はオフです。
- 予測値を出力する
- 分析により得られた偏回帰係数を説明変数にあてはめた予測値を出力する場合、このチェックボックスをオンにします。初期設定はオフです。
- 予測値の区間推定を出力する
- [予測値を出力する] がオンのときに指定できます。[信頼度] テキストボックスには50%以上99%以下の値を信頼度として入力できます。
- 回帰診断の統計量を出力する
- [予測値を出力する] がオンのときに指定できます。
- 不均一分散の検定を出力する
- [回帰診断の統計量を出力する] がオンのときに指定できます。
出力内容
| 度数の要約 | 有効ケース、無効ケース、全体の「サンプルサイズ」と「割合」が出力されます。度数を設定した場合にのみ出力されます。 |
|---|---|
| ケースの要約 | 有効ケース、目的変数のみ不明、説明変数のみ不明、ともに不明、全体の「サンプルサイズ」と「割合」 |
| 基本統計量 | 説明変数と目的変数の各変数の「サンプルサイズ」、「平均」、「不偏分散」、「標準偏差」、「最小値」、「最大値」 |
| 相関行列 | 目的変数の全体と各群における説明変数間の相関係数の行列 |
| 線形結合している変数 | 説明変数間で線形結合している変数のリスト |
| 変数選択の方法 | 変数選択に用いた方法と変数選択の基準値 |
| 回帰式の精度※1 | 変数選択過程もしくは最終ステップにおける回帰式の「重相関係数」、「自由度修正済み重相関係数」、それぞれの重相関係数から算出された「決定係数」、「自由度修正済み決定係数」、「ダービン=ワトソン比」、「AIC」、変数選択過程もしくは最終ステップで投入、除去された変数※1 |
| 回帰式の有意性(分散分析)※1 | 目的変数の全体変動を回帰変動と誤差変動に分解した分散分析表です。偏差平方和についてのF検定の結果も出力されます。 |
| 回帰式に含まれる変数(偏回帰係数・信頼区間等)※1 | 変数選択過程もしくは最終ステップの回帰式に含まれる各説明変数の「偏回帰係数」、「標準誤差」、「標準偏回帰係数」、「偏回帰係数の95%信頼区間」、「偏回帰係数の有意性の検定」の結果、「目的変数との相関」(単相関、偏相関)、「多重共線性の統計量」(トレランス、VIF) |
| 回帰式に含まれない変数※1 | 変数選択過程もしくは最終ステップの回帰式に含まれない各説明変数を回帰式に投入した場合の有意性を検定した結果 |
| 【グラフ】観測値×予測値※2 | X軸に観測値、Y軸に予測値をプロットした散布図 |
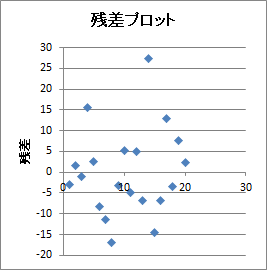
| 【グラフ】残差プロット※3 | 各ケースの残差(観測値と予測値の差)をプロットした散布図 |
| 予測値※2 | 目的変数の「観測値」と回帰式から算出された「予測値」 |
| 予測値の信頼区間※4 | 回帰式から算出された予測値の「95%信頼区間」 |
| 回帰診断※3 | 予測値と観測値との残差の分析として、「残差」、「標準化残差」、「スチューデント化残差」を出力します。影響力の分析として、「Cookの距離」と「てこ比」を出力します。 |
| 不均一分散の検定※5 | 帰無仮説:「各誤差項の分散は等しい」について、「Breusch-Pagan」の方法と「White」の方法により検定を行った結果が出力されます。 |
※1:ダイアログで[変数選択の過程を出力する]にチェックを入れた場合、ステップごとの値も出力します。ただし、「回帰式に含まれない変数」は「変数選択過程」にのみ出力されます。
※2:ダイアログで[予測値を出力する]にチェックを入れた場合に出力します。
※3:ダイアログで[回帰診断の統計量を出力する]にチェックを入れた場合に出力します。
※4:ダイアログで[予測値の区間推定を出力する]にチェックを入れた場合に出力します。
※5:ダイアログで[不均一分散の検定を出力する]にチェックを入れた場合に出力します。
スライドによる使い方の説明
エクセル統計の使い方(重回帰分析編) from Social Survey Research Information Co., Ltd.
参考文献
- 君山 由良, "重回帰分析の利用法", データ分析研究所, 2004.
- 田中 豊, 垂水 共之, 脇本 和昌, "パソコン統計解析ハンドブック 2 多変量解析編", 共立出版, 1984.
- 芳賀 敏郎, 橋本 茂司, "回帰分析と主成分分析", 日科技連出版社, 1980.>
- 村瀬 洋一, 高田 洋, 廣瀬 毅士, "SPSSによる多変量解析", Ohmsha, 2007.
- 柳井 晴夫, 高木 広文, "多変量解析ハンドブック", 現代数学社, 1986.
- 脇本 和昌, 垂水 共之,田中 豊, "パソコン統計解析ハンドブック 1 基礎統計編", 共立出版, 1984.
- SAS/STAT(R) 9.22 User's Guide.


