双対尺度法 : Dual Scaling
概要
双対尺度法は西里静彦が1982年に発表した分析法です。クロス集計表(分割表)で表される非計量的(質的)データを数量化し、解釈を容易にすることが目的です。
因子分析や数量化3類、コレスポンデンス分析と同様に複数の因子を抽出します。抽出される因子軸の数は、最大でも、「行数-1」か「列数-1」のどちらか少ない方となります。因子は寄与率の高いものから順に出力されます。各因子について行・列それぞれのカテゴリーの「最適重みベクトル」が計算されます。
処理対象データ
集計表形式
| データサイズ範囲 | 処理対象データ | ||||
|---|---|---|---|---|---|
| 行数 | 列数 | 行数×列数 | 数値 | 文字列 | 空白 |
| 3~3,000行 | 3~250列 | 10,000セル以下 | ○ | 欠 | 欠 |
※:○…処理可、×…処理不可、欠…0として処理
集計表概要
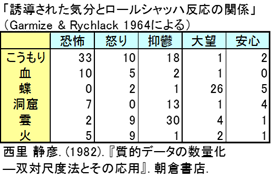
- 負の数を含まないこと
設定項目
Excelの[エクセル統計]タブから、[集計表の作成と分析]→[双対尺度法]もしくは[多変量解析]→[双対尺度法]を選択すると以下のダイアログが表示されます。
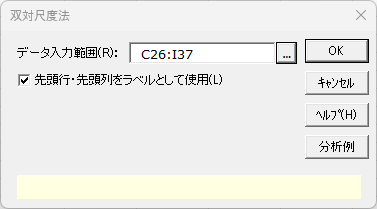
- データ入力範囲 必須
- クロス集計表の合計を除いたセル範囲を指定します。「空白」や「文字」のセルはゼロとして扱います。
- 先頭行・先頭列をラベルとして使用
- 入力範囲の先頭行および先頭列がラベルの場合、このチェックボックスをオンにします。初期設定はオンになっています。
出力内容
| クロス集計表 | データ入力範囲に指定したクロス集計表 |
|---|---|
| 各因子軸の解と検定 | 各因子の「相関比η2」、「寄与率」、「累積寄与率」、「カイ二乗値」、「自由度」、カイ二乗値の「P値」 |
| 最適重みベクトル:相関比による重み付けをしないもの | 相関比による重み付けをしていない各因子軸の最適重みベクトル |
| 最適重みベクトル:相関比による重み付けをしたもの | 上記の最適重みベクトルに相関比を掛けた各因子軸の最適重みベクトル |
| 【グラフ】第1軸×第2軸 | 第1軸と第2軸の最適重みベクトルを用いて作成したラベル付き散布図 |
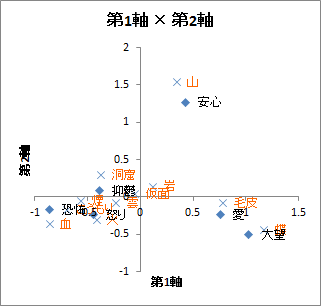
参考文献
集計表の作成と分析 その他の手法
- カテゴリカルデータの度数分布
- 適合度の検定 [度数分布表のカイ二乗検定]
- クロス集計表の作成と分析
- 独立性の検定 [クロス集計表のカイ二乗検定]
- フィッシャーの直接確率検定 [Fisher's exact probability Test]
- クロス集計表の残差分析
- リスク比とオッズ比
- コクラン=アーミテージ検定 [Cochran-Armitage Test]
- コクラン=マンテル=ヘンツェル検定 [Cochran-Mantel-Haenszel Test / 多層の2×2表の検定]
- 拡張マンテル検定 [Mantel-extension Test / 多層のk×2表の検定]
- マクネマー検定 [McNemar Test]
- グッドマン=クラスカルのガンマ [Goodman-Kruskal's gamma]
- グッドマン=クラスカルのタウ [Goodman-Kruskal's tau]
- カッパ係数
- コレスポンデンス分析
- 双対尺度法


