適合度の検定(度数分布表のカイ二乗検定) : Goodness-of-Fit Test
概要
n個の階級の度数分布において、i番目の階級の観測度数(Oi)と期待度数(Ei)が等しいといえるかどうかを検定します。帰無仮説は「観測度数は期待度数と比較して差がない」です。
分析例ファイルのダウンロード
適合度の検定を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
データベース形式
| データサイズ範囲 | 処理対象データ | ||||
|---|---|---|---|---|---|
| 行数 | 列数 | 数値 | 文字列 | 空白 | |
| 実測度数範囲 | 2~60行 | 1列 | ○ | 欠 | 欠 |
| 期待度数範囲 | 2~60行 | 1列 | ○ | × | × |
| 出力範囲 | 1行 | 1列 | - | - | - |
※:○…処理可、×…処理不可、欠…0として処理
データベース概要
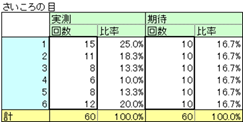
- 実測度数と期待度数の2つのデータが1列ずつあること
- 期待度数のデータには文字列、空白を含まないこと
- 期待度数は「度数データ」、「比率データ」どちらでも処理可
設定項目
Excelの[エクセル統計]タブから、[集計表の作成と分析]→[適合度の検定]を選択すると以下のダイアログが表示されます。
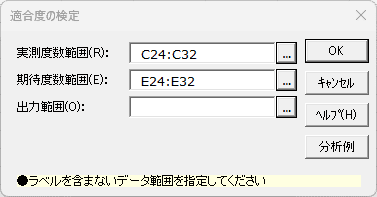
- 実測度数範囲 必須
- 1列の度数分布表の実測度数の範囲をラベルや合計を除いて指定します。実測度数範囲の「空白」や「文字」のセルはゼロとして扱います。
- 期待度数範囲 必須
- 1列の期待度数の範囲をラベルや合計を除いて指定します。「空白」や「文字」、「ゼロ」のセルを含む場合は計算を行いません。期待度数範囲に指定する内容は、過去の調査結果の度数でも相対度数でもどちらでも構いません。
- 出力範囲 必須
- 結果を出力するワークシート上の1セルを指定します。指定したセルを基準(左上セル)に結果を出力します。
出力内容
| カイ二乗値 | カイ二乗値 |
|---|---|
| 自由度 | カイ二乗分布の自由度(「階級の数-1」)が出力されます。 |
| P値 | カイ二乗分布の上側累積確率 |
| *:P < 0.05 **:P < 0.01 | P値が0.05未満なら"*"、0.01未満なら"**"が出力されます。 |
集計表の作成と分析 その他の手法
- カテゴリカルデータの度数分布
- 適合度の検定 [度数分布表のカイ二乗検定]
- クロス集計表の作成と分析
- 独立性の検定 [クロス集計表のカイ二乗検定]
- フィッシャーの直接確率検定 [Fisher's exact probability Test]
- クロス集計表の残差分析
- リスク比とオッズ比
- コクラン=アーミテージ検定 [Cochran-Armitage Test]
- コクラン=マンテル=ヘンツェル検定 [Cochran-Mantel-Haenszel Test / 多層の2×2表の検定]
- 拡張マンテル検定 [Mantel-extension Test / 多層のk×2表の検定]
- マクネマー検定 [McNemar Test]
- グッドマン=クラスカルのガンマ [Goodman-Kruskal's gamma]
- グッドマン=クラスカルのタウ [Goodman-Kruskal's tau]
- カッパ係数
- コレスポンデンス分析
- 双対尺度法


