グッドマン=クラスカルのタウ : Goodman-Kruskal's Tau
概要
ある2つの変数が原因と結果の関係であると考えた場合、従属変数(結果側)の予測誤差が、独立変数(原因側)の情報を加えて予測したらどれくらい減少するかを表したものを、誤差減少率(PRE)と言います。グッドマン=クラスカルのタウとは、クロス集計表から求めた誤差減少率です。
各行や各列で1セルにしか度数が認められない場合にタウは1となり、独立変数の値によって従属変数の値を100%予測できます。各行または各列ですべて度数が同じ場合にタウは0となり、独立変数と従属変数は独立しており因果関係は認められません。
分析例ファイルのダウンロード
グッドマン=クラスカルのタウを使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
集計表形式
| データサイズ範囲 | 処理対象データ | |||
|---|---|---|---|---|
| 行数 | 列数 | 数値 | 文字列 | 空白 |
| 2~60行 | 2~60列 | ○ | 欠 | 欠 |
※:○…処理可、×…処理不可、欠…0として処理
集計表概要

- 負の数を含まないこと
- データは整数であること
設定項目
Excelの[エクセル統計]タブから、[集計表の作成と分析]→[グッドマン=クラスカルのタウ]を選択すると以下のダイアログが表示されます。
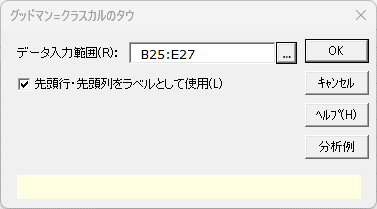
- データ入力範囲 必須
- クロス集計表の合計を除いたセル範囲を指定します。「空白」や「文字」のセルはゼロとして扱います。
- 先頭行・先頭列をラベルとして使用
- 入力範囲の先頭行および先頭列がラベルの場合、このチェックボックスをオンにします。初期設定はオンになっています。
出力内容
| 観測度数 | データ入力範囲に指定されたクロス集計表 |
|---|---|
| 質的分散 | 行が従属変数の場合の各列の「質的分散」と、列が従属変数の場合の各行の「質的分散」が出力されます。 |
| Goodman-Kruskal's tau | 行が従属変数の場合と列が従属変数の場合の「Goodman-Kruskal's tau」が出力されます。 |
参考文献
集計表の作成と分析 その他の手法
- カテゴリカルデータの度数分布
- 適合度の検定 [度数分布表のカイ二乗検定]
- クロス集計表の作成と分析
- 独立性の検定 [クロス集計表のカイ二乗検定]
- フィッシャーの直接確率検定 [Fisher's exact probability Test]
- クロス集計表の残差分析
- リスク比とオッズ比
- コクラン=アーミテージ検定 [Cochran-Armitage Test]
- コクラン=マンテル=ヘンツェル検定 [Cochran-Mantel-Haenszel Test / 多層の2×2表の検定]
- 拡張マンテル検定 [Mantel-extension Test / 多層のk×2表の検定]
- マクネマー検定 [McNemar Test]
- グッドマン=クラスカルのガンマ [Goodman-Kruskal's gamma]
- グッドマン=クラスカルのタウ [Goodman-Kruskal's tau]
- カッパ係数
- コレスポンデンス分析
- 双対尺度法


