多次元尺度法 : Multi-Dimentional Scaleing
概要
多次元尺度法は、多変量データから距離を計算し、高次元データを低次元データにマッピングします。類似したものを見つけ出します。
多変量データと類似度行列データとに対応しています。分析の結果、座標値と散布図が求められます。
多変量データにおいては、1つでも変数の欠けているケースは分析実行時に自動的に除かれて計算されます。
分析例ファイルのダウンロード
多次元尺度法を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
データベース形式
| データサイズ範囲 | 処理対象データ | |||||
|---|---|---|---|---|---|---|
| 行数 | 列数 | 数値 | 文字列 | 空白 | ||
| 個体の 布置 |
データラベル | 3~1,000行 | 1列 | ○ | ○ | ○ |
| 分析に用いる変数 | 3~1,000行 | 2~100列 | ○ | 欠 | 欠 | |
| 変数の布置※1 | 分析に用いる変数 | 3~1,000行 | 3~100列 | ○ | 欠 | 欠 |
※1:変数の布置をプロットする場合は、データラベルの情報を分析には用いません
行列形式
| データサイズ範囲 | 処理対象データ | 行数 | 列数 | 数値 | 文字列 | 空白 |
|---|---|---|---|---|
| 2~300行 | 2~300列 | ○ | × | ×※2 |
※:○…処理可、×…処理不可、欠…欠損値として除く
※2:対角要素のみ空白は0として処理
行列形式概要
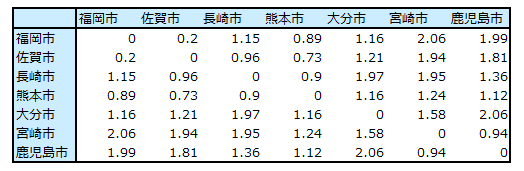
- 2行2列以上の行列であること
- 行列は正方行列かつ対称行列であること
- 対角要素は0または空白であること
- 非計量の場合は、対角以外の要素が0でないこと
設定項目
Excelの[エクセル統計]タブから、[多変量解析]→[多次元尺度法]もしくは[多次元尺度法(行形式)]を選択すると以下のダイアログが表示されます。入力データがデータベース形式の場合について説明します。
多次元尺度法(データベース形式) 「変数」タブ
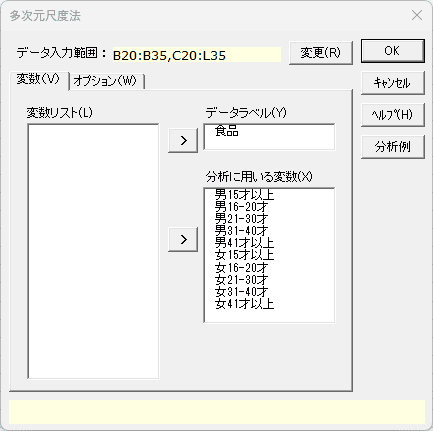
- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力範囲のダイアログが表示されるので、データ入力範囲を設定して [戻る] ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- データラベル
- [変数リスト] から [データラベル]の変数を設定します。
- 分析に用いる変数 必須
- [変数リスト]から [分析に用いる変数] を設定します。
多次元尺度法(データベース形式) 「オプション」タブ
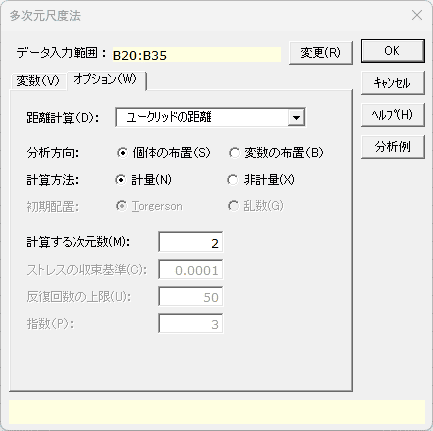
- 距離計算 必須
- 距離計算として [ユークリッドの距離]、[平方ユークリッドの距離]、[ミンコフスキーの距離]、[相関係数]、[パターン類似度] のいずれかを選択します。
- 分析方向 必須
- 分析方向として [個体の布置] と [変数の布置] のいずれかを選択します。
- 計算方法 必須
- 計算方法として [計量] と [非計量] のいずれかを選択します。
- 初期配置
- 初期配置として [Torgerson] と [乱数] のいずれかを選択します。計算方法で[非計量]のチェックをオンにしたときに選択することができます。
- 計算する次元数 必須
- 計算する次元数を設定します。初期設定は「2」になっています。
- ストレスの収束基準
- ストレスの収束基準を設定します。初期設定は「0.0001」になっています。計算方法で[非計量] のチェックをオンにしたときに選択することができます。
- 反復回数の上限
- 反復回数の上限を設定します。初期設定は「50」になっています。計算方法で[非計量] のチェックをオンにしたときに選択することができます。
- 指数
- 距離計算で[ミンコフスキーの距離] を選択した場合に指数を設定します。初期設定は「3」になっています。
多次元尺度法(行列形式)
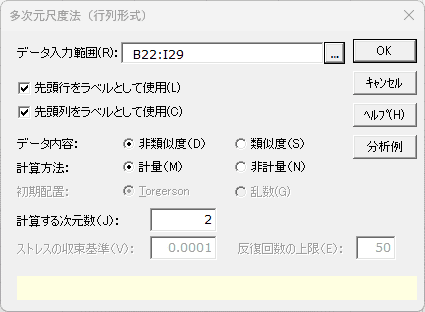
- データ入力範囲 必須
- 300行×300列までの対称な正方行列を指定します。対角要素はすべて0である必要があります。
- 先頭行をラベルとして使用
- 入力範囲の先頭行が変数ラベルの場合、このチェックボックスをオンにします。初期設定はオンになっています。
- 先頭列をラベルとして使用
- 入力範囲の先頭列が変数ラベルの場合、このチェックボックスをオンにします。初期設定はオンになっています。
- データ内容 必須
- データ内容として [非類似度] と [類似度] のいずれかを選択します。
- 計算方法 必須
- 計算方法として [計量] と [非計量] のいずれかを選択します。
- 初期配置
- 初期配置として [Torgerson] と [乱数] のいずれかを選択します。計算方法で[非計量]のチェックをオンにしたときに選択することができます。
- 計算する次元数 必須
- 計算する次元数を設定します。初期設定は「2」になっています。
- ストレスの収束基準
- ストレスの収束基準を設定します。初期設定は「0.0001」になっています。計算方法で[非計量] のチェックをオンにしたときに選択することができます。
- 反復回数の上限
- 反復回数の上限を設定します。初期設定は「50」になっています。計算方法で [非計量] のチェックをオンにしたときに選択することができます。
出力内容
データベース形式
| ケースの要約 | 有効ケース、目的変数のみ不明、説明変数のみ不明、ともに不明、全体の「サンプルサイズ」と「割合」 |
|---|---|
| 基本統計量 | 説明変数と目的変数の各変数の「サンプルサイズ」、「平均」、「不偏分散」、「標準偏差」、「最小値」、「最大値」 |
| 相関行列 | 目的変数の全体と各群における説明変数間の相関係数の行列 |
| 設定内容 | ダイアログで設定した「距離計算」、「分析方向」、「計算方法」、「初期配置※2」、「計算する次元数」、「ストレスの収束基準※2」、「反復回数の上限※2」、「指数※3」 |
| 距離行列 | 対象間の距離行列 |
| 分析対象行列 | 分析対象となる行列 |
| 固有値※1 | 各次元に対する固有値 |
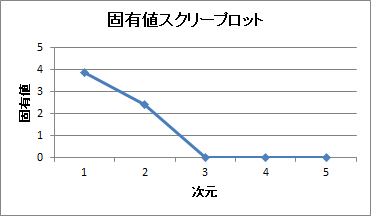
| 【グラフ】固有値スクリープロット※1 | 次元1から順に正の固有値の値を線でつないだ折れ線グラフ |
| 固有ベクトル※1 | 各次元に対応する固有ベクトル |
| ストレス※2 | 次元ごとのストレス値 |
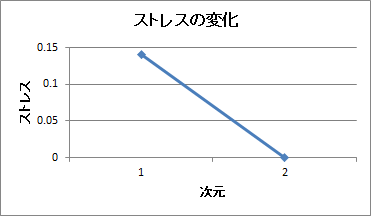
| 【グラフ】ストレスの変化※2 | 次元1から順にストレスの値を線でつないだ折れ線グラフ |
| 投影結果 | 各個体をマッピングする際の座標 |
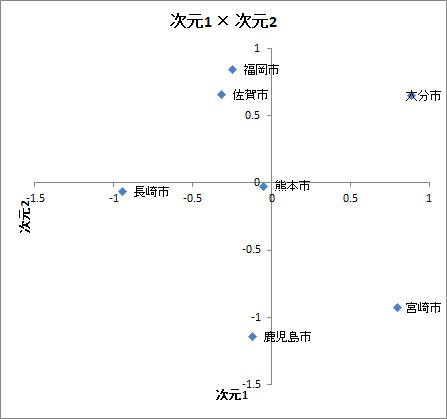
| 【グラフ】シミュレーション(次元1×次元2) | 各個体を2次元空間にマッピングしたグラフです。シミュレーションの「回転角度」に数値を入力すると、入力した数値だけ回転させたグラフが描かれます。 |
| 投影結果(回転後) | 各個体の座標をシミュレーションの「回転角度」に入力した数値だけ回転させた後の座標 |
※1:ダイアログで[計算方法]を[計量]とした場合
※2:ダイアログで[計算方法]を[非計量]とした場合
※3:ダイアログで[距離計算]を[ミンコフスキーの距離]とした場合
行列形式
| 設定内容 | ダイアログで設定した「距離計算」、「分析方向」、「計算方法」、「初期配置※2」、「計算する次元数」、「ストレスの収束基準※2」、「反復回数の上限※2」 |
|---|---|
| 距離行列 | 対象間の距離行列 |
| 二重中心化した距離行列 | 二重中心化した距離行列 |
| 固有値※1 | 各次元に対する固有値 |
| 【グラフ】固有値スクリープロット※1 | 次元1から順に正の固有値の値を線でつないだ折れ線グラフ |
| 固有ベクトル※1 | 各次元に対応する固有ベクトル |
| ストレス※2 | 次元ごとのストレス値 |
| 【グラフ】ストレスの変化※2 | 次元1から順にストレスの値を線でつないだ折れ線グラフ |
| 投影結果 | 各個体をマッピングする際の座標 |
| 【グラフ】シミュレーション(次元1×次元2) | 各個体を2次元空間にマッピングしたグラフです。シミュレーションの「回転角度」に数値を入力すると、入力した数値だけ回転させたグラフが描かれます。 |
| 投影結果(回転後) | 各個体の座標をシミュレーションの「回転角度」に入力した数値だけ回転させた後の座標 |
※1:ダイアログで[計算方法]を[計量]とした場合
※2:ダイアログで[計算方法]を[非計量]とした場合
参考文献
- 岡田 彬訓,今泉 忠, "パソコン多次元尺度構成法", 共立出版株式会社, 1994
- Sammon JW, "A nonlinear mapping for data structure analysis" IEEE Trans. Comput., 18, 401–409. 1969


