主成分分析 : Principal Component Analysis
概要
主成分分析とは複数変数のデータのばらつき傾向から、少数の合成された新たな変数(主成分)を求める手法です。
体力テストを例にとると、第1主成分として基礎体力、第2主成分として俊敏性を示す主成分が得られたとします。次に各主成分について体力テスト毎の主成分負荷量を見ることで、それぞれの体力テストの結果が基礎体力を強く表しているのか、俊敏性を強く表しているのか推定することが出来ます。
主成分分析では固有値という指標が同時に求められますが、これは主成分の重要度を示し、第1主成分が最も高く、第2、第3と段々小さくなります。次に主成分得点を見ることで、各個人が基礎体力に優れているのか、俊敏性に優れているのか見ることができます。
分析例ファイルのダウンロード
主成分分析を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
データベース形式
| データサイズ範囲 | 処理対象データ | ||||
|---|---|---|---|---|---|
| 行数 | 列数 | 数値 | 文字列 | 空白 | |
| データラベル※1 | 3~60,000行 | 1列 | ○ | ○ | ○ |
| 分析に用いる変数 | 3~60,000行 | 2~100列※2 | ○ | 欠 | 欠 |
※:○…処理可、×…処理不可、欠…欠損値として除く
※1:データラベルは未入力でも処理可
※2:分析に用いる変数が2つ以上あること
設定項目
Excelの[エクセル統計]タブから、[多変量解析]→[主成分分析]を選択すると以下のダイアログが表示されます。
「変数」タブ
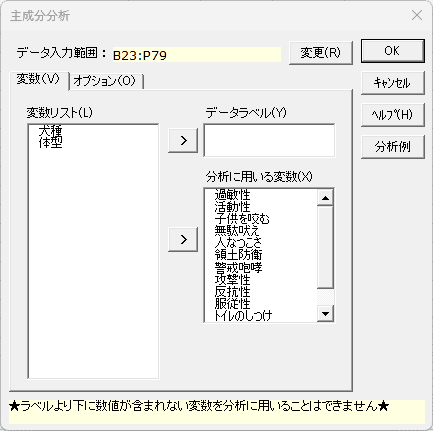
- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力範囲のダイアログが表示されるので、データ入力範囲を設定して [戻る] ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- データラベル
- [変数リスト]からデータラベルの変数を設定します。
- 分析に用いる変数 必須
- [変数リスト]から分析に用いる変数を設定します。
「オプション」タブ
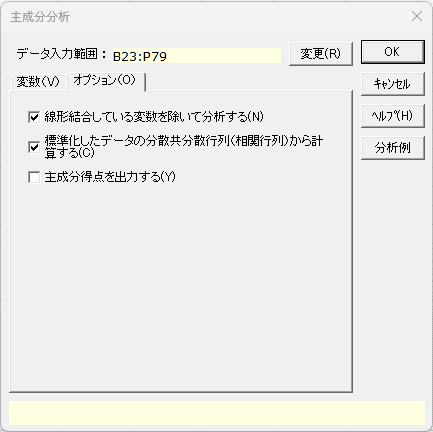
- 線形結合している変数を除いて分析する
- 線形結合している変数を最初に除いてから分析する場合、このチェックボックスをオンにします。初期設定はオンです。
- 標準化したデータの分散共分散行列(相関行列) から計算する
- 変数間で単位が異なる場合、このチェックボックスをオンにすることで、元データを標準化して分析した場合と同じ解になります。初期設定はオフです。
- 主成分得点を出力する
- 主成分得点を出力する場合、このチェックボックスをオンにします。初期設定はオフです。
出力内容
| ケースの要約 | 有効ケース、不明ケース、全体の「サンプルサイズ」と「割合」 |
|---|---|
| 基本統計量 | 各変数の「サンプルサイズ」、「平均」、「不偏分散」、「標準偏差」、「最小値」、「最大値」 |
| 分析対象行列 | 変数間の分散共分散または相関係数の行列 |
| 線形結合している変数 | 変数間で線形結合している変数のリスト |
| 固有値表 | 各主成分の「固有値」、「寄与率」、「累積寄与率」 |
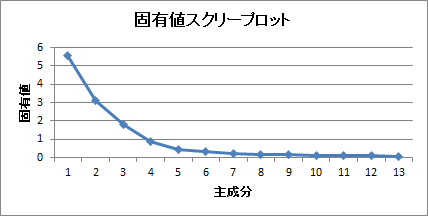
| 【グラフ】固有値スクリープロット | 第1主成分から順に固有値の値を線でつないだ折れ線グラフ |
| 固有ベクトル | 各主成分の固有ベクトル |
| 主成分負荷量 | 各主成分の各変数への主成分負荷量 |
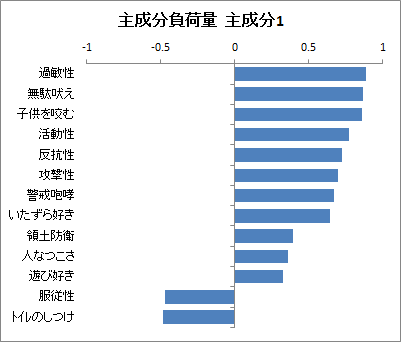
| 【グラフ】主成分負荷量 | 各変数に対する負荷量を横棒で表したグラフです。最大4つまで出力されます。 |
| 【グラフ】主成分1×主成分2 | 主成分1の因子負荷量を横軸に、主成分2の主成分負荷量を縦軸にとり変数をプロットしたラベル付き散布図です。因子が2つ以上ある場合にのみ出力されます。 |
| 主成分得点※1 | 各主成分の各ケースの主成分得点 |
※1:ダイアログで[主成分得点を出力する]にチェックを入れた場合に出力します。
参考文献
- 木下 栄蔵, "わかりやすい数学モデルによる多変量解析入門", 啓学出版, 1987
- 芳賀 敏郎, 橋本 茂司, "回帰分析と主成分分析", 日科技連出版社, 1980.
- 村瀬 洋一, 高田 洋, 廣瀬 毅士, "SPSSによる多変量解析", オーム社, 2007.
- 柳井 晴夫, 高木 広文, "多変量解析ハンドブック", 現代数学社, 1986.


