例題：

ある学校の1組と2組の算数のテストの平均点を比較します。1組の生徒30人の平均点は75点、標準偏差は5点、2組の生徒32人の平均点は70点、標準偏差は8点でした。この結果から、1組と2組の算数のテストの平均点に差はあると言えるでしょうか。

1. 仮説を立てる

帰無仮説は「1組と2組の算数のテストの平均点は等しい」とします。したがって、対立仮説は「1組と2組の算数のテストの平均点には差がある」となります。

2. 有意水準を設定する

＝0.05とします。

3. 適切な検定統計量を決める

この実験では母分散が分からないので、不偏分散を用いる統計量tを使います。2標本の平均値の差を検定するため、統計量tは次の式から求めます。は1群目の標本平均、は1群目のサンプルサイズ、は2群目の標本平均、は2群目のサンプルサイズ、はプールした分散を表します。


4. 棄却ルールを決める

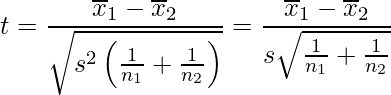
この検定で使用する分布は自由度「30+32-2=60」の「t分布」になります。また、1組と2組の算数のテストの平均点に差があるかどうかを調べることが目的なので、両側検定を行います。統計数値表からの値を読み取ると「2.000」となっています。

5. 検定統計量を元に結論を出す

24-3章で学んだように、まず2つの標本をプールした（まとめた）分散を算出します。



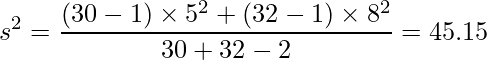
この値を統計量tの式に代入すると次のようになります。



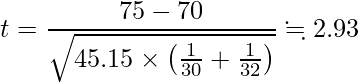
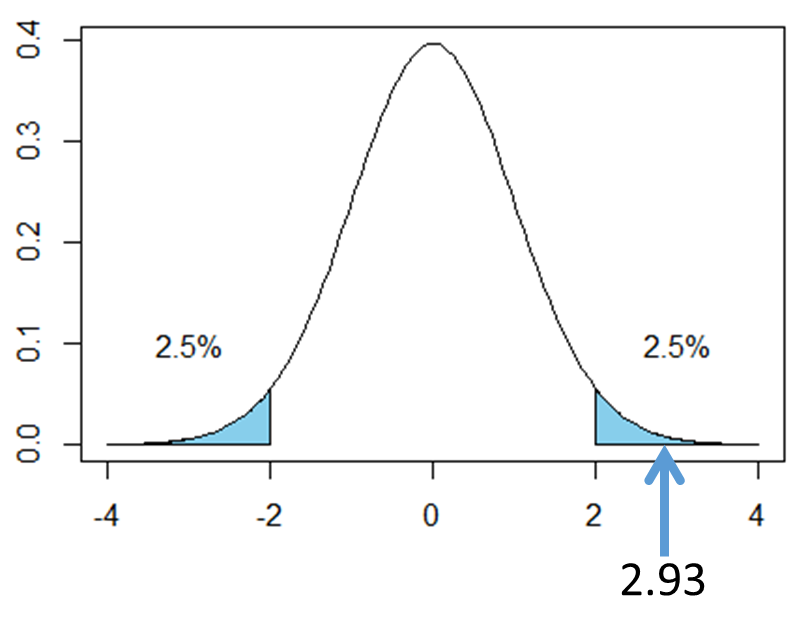
次の図は自由度60のt分布を表したものです。t=2.93は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%の両側検定において、帰無仮説は棄却され、対立仮説が採択される」という結果になります。つまり、「1組と2組の算数のテストの平均点には差がある」と結論づけられます。

【コラム】母分散が等しいと仮定できる場合とできない場合

この章で説明した対応のない2標本t検定のための統計量tを求める式は、2標本の母分散が等しいという前提のもとに使います。もし2標本の母分散が等しいと仮定できない場合、「ウェルチのt検定」を使います。そのため、2つの標本の母分散が等しいかどうか分からない場合、等分散性を検定し、その結果を元にどちらの式を使うべきかを判断するようにと多くの書籍に記載されてきました。

ただし近年では、等分散性の検定をせず、はじめから「ウェルチのt検定」を使うケースが増えてきているようです。例えばRを用いて対応のない2標本t検定をおこなった場合、デフォルトで「ウェルチのt検定」の結果が出力されます。また、エクセル統計もデフォルトは「ウェルチのt検定」となっています。