母平均の差の検定 : Hypothesis Testing for the Difference in Means
概要
母集団からサンプリングした2標本のサンプルサイズ( \(n_1,\ n_2\) )、平均値( \(x_1,\ x_2\) )、不偏分散( \(s_1^2,\ s_2^2\) )をもとに、2群の母集団の平均値( \(\mu_1,\ \mu_2\) )が等しいという帰無仮説を検定します。「 \(\mu_1 \neq \mu_2\) 」を対立仮説に設定する場合、両側P値より有意性を判定します。「 \(\mu_1 > \mu_2\) 」あるいは「 \(\mu_1 < \mu_2\) 」を対立仮説に設定する場合、片側P値より有意性を判定します。
対応のない2標本のデータがそれぞれ1列ずつにまとめられている場合、「母平均の差の検定(表形式)」を使用してください。2標本のデータが観測値1列と標本を識別する変数1列にまとめられている場合、「母平均の差の検定(データベース形式)」を使用してください。
分析例ファイルのダウンロード
母平均の差の検定を使用する際のデータの形式やダイアログの指定方法、出力結果などを以下のExcelファイルからご確認いただけます。ダウンロードしてご参照ください。この分析例ファイルは、製品をご購入された場合にも自動でインストールされます。
なお、エクセル統計の無料体験版では、分析例ファイルのデータを実際に分析してみることができます。
処理対象データ
「表形式」、「要約データ形式」、「データベース形式」のデータを計算することができます。
表形式
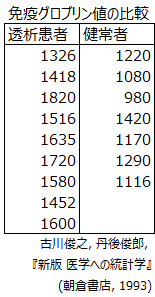
- 先頭行を変数のラベルとして扱います。
- 2行目以降を各変数の観測値として計算に用います。
- 列ごとに欠損値を除いて計算を行います。
先頭行のラベルを除いたセル範囲について、行数と列数の上限、扱えるデータの種類は次の通りです。
データサイズ(表形式)
- 行数2~60,000行
- 列数1~255列
データ内容(表形式)
- 数値○:処理可
- 文字列欠損値として除く
- 空白欠損値として除く
要約データ形式
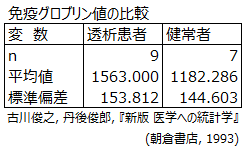
- 先頭行を変数のラベルとして扱います。
- 2行目以降を「サンプルサイズ」、「平均値」、「標準偏差」として計算に用います。
- 欠損値がある場合は計算を行いません。
- 「サンプルサイズ」が0または負の場合は計算を行いません。
- 「標準偏差」が負の場合は計算を行いません。
先頭行のラベルを除いたセル範囲について、行数と列数の上限、扱えるデータの種類は次の通りです。
データサイズ(要約データ形式)
- 行数3行
- 列数1~255列
データ内容(要約データ形式)
- 数値○:処理可
- 文字列×:処理不可
- 空白×:処理不可
データベース形式

- 先頭行を変数のラベルとして扱います。
- 2行目以降を各変数の観測値として計算に用います。
- 「標本を識別する変数」を1列含みます。このデータ例では、「グループ」が「標本を識別する変数」です。
- 「標本を識別する変数」に含まれるカテゴリーは2種類である必要があります。
- 「標本を識別する変数」が欠損値となっている行をデータ全体から除いて計算を行います。
- 「検定を行う変数」を1列以上含みます。このデータ例では、「観測値」が「検定を行う変数」です。複数列指定した場合は同時に検定を行うことができます。
- 「検定を行う変数」に欠損値が含まれる場合、列ごとに欠損値を除いて計算を行います。
先頭行のラベルを除いたセル範囲について、行数と列数の上限、扱えるデータの種類は次の通りです。
データサイズ(標本を識別する変数)
- 行数2~60,000行
- 列数1列
データ内容(標本を識別する変数)
- 数値○:処理可
- 文字列○:処理可
- 空白欠損値として除く
データサイズ(検定を行う変数)
- 行数2~60,000行
- 列数1~250列
データ内容(検定を行う変数)
- 数値○:処理可
- 文字列欠損値として除く
- 空白欠損値として除く
設定項目
Excelの[エクセル統計]タブから、[2標本の比較]→[母平均の差の検定(表形式)]もしくは[2標本の比較]→[母平均の差の検定(データベース形式)]を選択すると以下のダイアログが表示されます。
表形式・要約データ形式
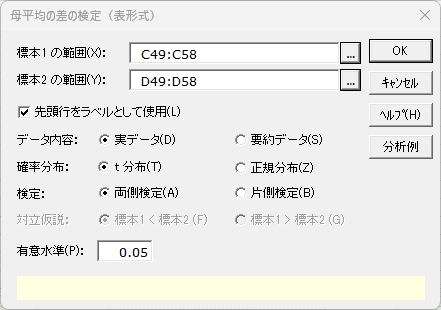
- 標本 1 の範囲・標本2 の範囲 必須
- 1 列から255 列までの実データ(量的データ)または要約データの範囲を指定します。
実データの場合、ラベル行を除いて各列に3 個以上のデータが必要です。「空白」や「文字」のデータは計算から除かれます。
要約データの場合、上から変数(列)ごとに、サンプルサイズ、平均、標準偏差の3行にまとめられている必要があります。 - 先頭行をラベルとして使用
- 入力範囲の先頭行が変数ラベルの場合、このチェックボックスをオンにします。初期設定はオンになっています。
- データ内容 必須
- データの内容に合わせて[実データ]と[要約データ]のいずれかを選択します。
- 確率分布 必須
- [t 分布]と[正規分布]のいずれかを選択します。
- 検定 必須
- [両側検定]と[片側検定]のいずれかを選択します。
- 対立仮説 必須
- 検定で[片側検定]を選択した場合、対立仮説として[標本1 < 標本2]と[標本1 > 標本2]のいずれかを選択します。
- 有意水準 必須
- 母平均の差の検定の有意水準を0.001以上0.2以下で設定します。初期設定は0.05です。
データベース形式 「変数」タブ
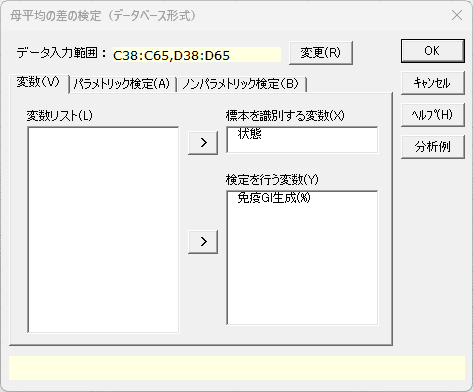
- データ入力範囲 必須
- データ入力範囲の変更を行う場合、[変更]ボタンを選択します。データ入力のダイアログが表示されるので、データ入力範囲を設定して[変更]ボタンを選択します。なお、データ入力範囲の先頭行は変数名となります。
- 標本を識別する変数 必須
- [変数リスト]から標本を識別する変数を1つ設定します。
- 検定を行う変数 必須
- [変数リスト]から検定を行う変数を設定します。
データベース形式 「パラメトリック検定」タブ
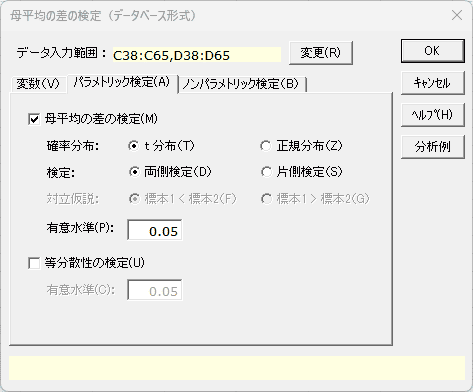
- 母平均の差の検定
- 母平均の差の検定を行う場合はオンにします。
- 確率分布
- [t分布]と[正規分布]のいずれかを選択します。
- 検定
- [両側検定]と[片側検定]のいずれかを選択します。
- 対立仮説
- 検定で[片側検定]を選択した場合、対立仮説として[標本1 < 標本2]と[標本1 > 標本2]のいずれかを選択します。
- 有意水準
- 等分散性の検定の有意水準を0.001以上0.2以下で設定します。初期設定は0.05です。
- 等分散性の検定
- 等分散性の検定を行う場合はオンにします。
- 有意水準
- 有意水準を0.001以上0.2以下で設定します。初期設定は0.05です。
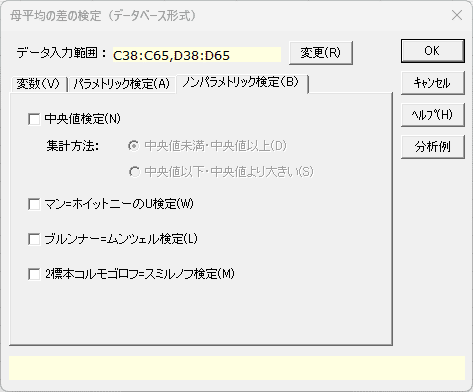
- [中央値検定]、[マン=ホイットニーのU検定]、[ブルンナー=ムンツェル検定]、[2標本コルモゴロフ=スミルノフ検定]の中から出力する検定をオンにします。中央値検定を選択した場合、[中央値未満・中央値以上]か[中央値以下・中央値より大きい]のいずれかを選択します。
データベース形式 「ノンパラメトリック検定」タブ
出力内容
メニュー「母平均の差の検定(表形式)」において標本1と標本2に複数の変数を指定した場合、すべての変数の組み合わせについて検定を行います。
| 基本統計量 | 各標本それぞれの「有効サンプルサイズ」、「平均※1※2」、「不偏分散※1※2」、「標準偏差※1※2」、「標準誤差※1※2」、「中央値※3」、「平均順位※4」、「統計量:U※4」 |
|---|---|
| 等分散性の検定(両側検定)※2 | 帰無仮説:「2標本の母分散は等しい」をF分布に従う統計量を用いて検定した結果 |
ダイアログにて[確率分布]を[t分布]とした場合※1
| 平均の差と効果量 | 2標本の「平均の差」、「効果量(Cohen's d)」、「効果量(Hedges' g)」が出力されます。効果量はそれぞれ「効果量(観測値)」と「効果量(ランク化)」が出力されます。「効果量(観測値)」は入力されたデータから算出された値、「効果量(ランク化)」は入力されたデータに順位付けしたものから算出された値です。 |
|---|---|
| 母平均の差の95%信頼区間 t推定 | t分布に基づく2標本の母平均の差の95%信頼区間の「下限値」と「上限値」 |
| 母平均の差の95%信頼区間 Welchの方法 | Welchの方法による2標本の母平均の差の95%信頼区間の「下限値」と「上限値」 |
| 母平均の差の検定 t検定 | 帰無仮説:「2標本の母平均は等しい」について、t分布に従う統計量を用いて検定した結果が出力されます。「観測値」と「ランク化」されたデータのそれぞれについて結果が出力されます。 |
| 母平均の差の検定 Welchの方法 | 帰無仮説:「2標本の母平均は等しい」について、t分布に従う統計量を用いて検定した結果が出力されます。統計量はWelchの方法により計算され、小数点以下を含む自由度に対応した正確なP値が出力されます。 |
| 検出力 | 母平均の差の検定のそれぞれについての検出力。計算に用いている効果量はHedges' gです。 |
ダイアログにて[確率分布]を[正規分布]とした場合※1
| 平均の差と効果量 | 2標本の「平均の差」、「効果量(Cohen's d)」、「効果量(Hedges' g)」 |
|---|---|
| 母平均の差の95%信頼区間 | 正規分布に基づく2標本の母平均の差の95%信頼区間の「下限値」と「上限値」 |
| 母平均の差の検定 | 帰無仮説:「2標本の母平均は等しい」について、正規分布に従う統計量を用いて検定した結果 |
| 検出力 | 母平均の差の検定の検出力。計算に用いている効果量はHedges’ gです。 |
ノンパラメトリック検定(メニュー「母平均の差の検定(データベース形式)」を実行した場合のみ)
| 中央値検定※3 | 算出された「全体の中央値」を用いて2行×2列の分割表を出力します。分割表から「独立性の検定」、「Yatesの補正」、「Fisherの直接確率(両側P値)」、「Fisherの直接確率(片側P値)」の結果を出力します。 |
|---|---|
| マン=ホイットニーのU検定※4 | 統計数値表による結果と正規化検定の結果が出力されます。詳細は、「マン=ホイットニーのU検定」を参照してください。 |
| ブルンナー=ムンツェル検定※5 | 全データに割り当てられた順位と、各標本内での順位からブルンナー=ムンツェル検定を行った結果を出力します。詳細は、「ブルンナー=ムンツェル検定」を参照してください。 |
| 2標本コルモゴロフ=スミルノフ検定※6 | 累積相対度数の「最大差」と「統計量KS」からコルモゴロフ=スミルノフ検定を行なった結果を出力します。詳細は、「2標本コルモゴロフ=スミルノフ検定」を参照してください。 |
※1:「データベース形式」で[母平均の差の検定]をチェックした場合に出力されます。
※2:「データベース形式」で[等分散性の検定]をチェックした場合に出力されます。
※3:「データベース形式」で[中央値検定]をチェックした場合に出力されます。
※4:「データベース形式」で[マン=ホイットニーのU検定]をチェックした場合に出力されます。
※5:「データベース形式」で[ブルンナー=ムンツェル検定]をチェックした場合に出力されます。
※6:「データベース形式」で[2標本コルモゴロフ=スミルノフ検定]をチェックした場合に出力されます。


