母平均の区間推定における必要なサンプルサイズの計算フォーム
2017/12/19
カテゴリ:Tips
これから集めるサンプルにおける何らかの測定値の平均値が、母集団のそれとあまり変わらないようにしたい場合、 サンプルの平均値がある程度の誤差範囲内で収まるために必要なサンプルサイズを、誤差、信頼度、標準偏差を指定することで求めることができます。
入力には半角数字を用いて、それぞれの範囲内の値で指定してください。入力した値によっては計算に時間がかかる場合があります。その場合はブラウザの「読み込み中止」を選択してください。ページ最下部にあるExcel ファイルでも同じ計算を実行することができますので、ダウンロードしてお試しください。 → ダウンロードへ移動する
誤差(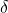 :デルタ)
:デルタ)
母平均に対するサンプル平均が、上下にどの程度の範囲内に収まって欲しいかを表します。
信頼度(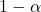 )
)
例えば、誤差を5、信頼度を90%としたとき、これは100回中90回は サンプル平均と母平均との差が±5の範囲内に収まることを意味します。
標準偏差(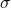 :シグマ)
:シグマ)
今、母集団の分散はわかりませんが、母集団の分散がわからないからと言ってその値を設定せずに サンプルサイズを設計することはできません。 標準偏差の値は、予備調査のデータや過去に行われた類似調査のデータ、 または何らかの情報に基づく予測値を用います。
サンプルサイズ
母分散がわからない場合の母平均の区間推定は以下の式で行われます。
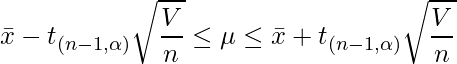
ここで、![]() (ミュー)は母平均、
(ミュー)は母平均、![]() はサンプル平均、
はサンプル平均、
![]() は1−信頼度、
は1−信頼度、![]() はサンプルサイズ、
はサンプルサイズ、![]() は不偏分散、
は不偏分散、
![]() は自由度
は自由度![]() のt分布の両側100P%点を表します。
のt分布の両側100P%点を表します。
このとき区間幅は
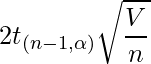
であり、この式には確率変数 ![]() が含まれていることから、
区間幅の期待値が一定値
が含まれていることから、
区間幅の期待値が一定値![]() 以下となるようにサンプルサイズを設計します。
以下となるようにサンプルサイズを設計します。
(1) 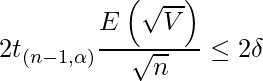
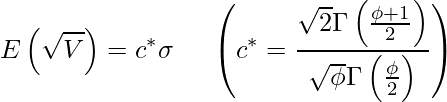
と変形することができます(参考文献を参照)。
![]() は母標準偏差、
は母標準偏差、![]() はガンマ関数で、このとき
はガンマ関数で、このとき![]() (ファイ)は
(ファイ)は![]() です。
です。
これを(1)式に戻し、さらにフォームに入力した標準偏差![]() を用いて
を用いて![]() とすると、
とすると、
(2) 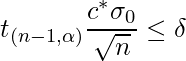
となります。ここで
とおきます。![]() は標準正規分布の上側100P%点です。
これを用いて(2)式を
は標準正規分布の上側100P%点です。
これを用いて(2)式を![]() について解くと、
について解くと、
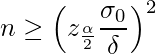
となります。この式の右辺を初期値として![]() を1ずつ大きくしていき、(2)式を満たす最小の
を1ずつ大きくしていき、(2)式を満たす最小の![]() が必要なサンプルサイズとなります。
が必要なサンプルサイズとなります。
誤差を変化させたときのサンプルサイズの変化
信頼度と標準偏差の値を固定して誤差の値を変化させてみると、上のグラフのように誤差を小さくするほど必要なサンプルサイズが増えることが見て取れます。
信頼度を変化させたときのサンプルサイズの変化
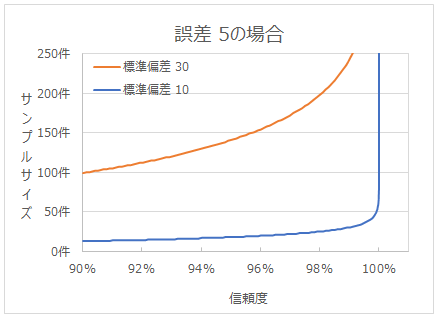
誤差と標準偏差の値を固定して信頼度の値を変化させてみると、 上のグラフのように信頼度を高くするほど必要なサンプルサイズが増えることが見て取れます。
標準偏差を変化させたときのサンプルサイズの変化
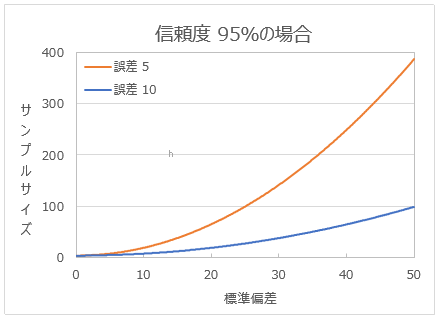
誤差と信頼度の値を固定して標準偏差の値を変化させてみると、 上のグラフのように標準偏差を大きくするほど必要なサンプルサイズが増えることが見て取れます。
ダウンロード
この統計TipのExcelファイルのダウンロードはこちらから → tips_16.xlsm
※ このファイルはサンプルサイズを計算するためのマクロを含んでいます。
参考文献
関連記事
- Tips|母比率の区間推定における必要なサンプルサイズの計算フォーム
- Tips|2標本の母平均の差の区間推定における必要なサンプルサイズの計算フォーム
- コラム「統計備忘録」|幾つデータが必要か?―平均値の差の検定
- コラム「統計備忘録」|幾つデータが必要か?―比率の差の検定
- コラム「統計備忘録」|幾つデータが必要か?―相関係数の有意性検定
- コラム「統計備忘録」|幾つデータが必要か?―測定の信頼性による補正
- コラム「統計備忘録」|バーに入ってきたビル・ゲイツ
- コラム「統計備忘録」|mの分布━標本平均と中心極限定理
- コラム「統計備忘録」|平均値と統計法
- コラム「統計備忘録」|平均値と中央値の違い









