公認会計士 論文式試験の選択問題(統計学)を解く ~その1~
2017/12/04
カテゴリ:公認会計士(統計学)
概要
この記事は、平成28年公認会計士論文試験の統計学分野の選択問題(第8問)を解いたものです。 統計学の時間で一通り勉強すれば、第8問はすべて解けるようになります。
記事一覧
目次
問題1
■問1:ア
正規分布を用いた信頼区間の推定に関する問題です。
問題文より、器具Aの寿命は次のような分布であることがわかります。
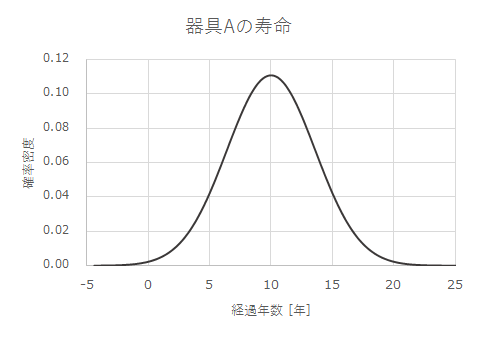
![]() のもとで、
のもとで、![]() を計算します。これは、次の図の青色で表される部分の面積です。
を計算します。これは、次の図の青色で表される部分の面積です。
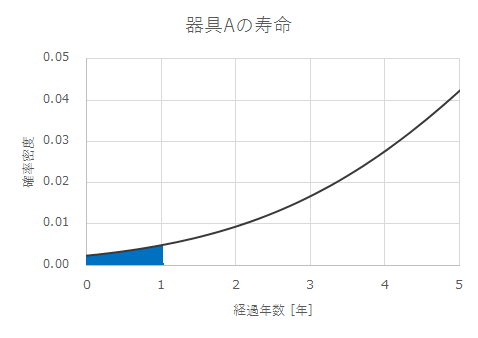
寿命が正規分布に従うことから、正規分布表を用いて計算することができます。最初に、![]() を標準化します。
を標準化します。
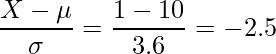
標準正規分布表より、求める確率は![]() です。
です。
しかしながら、この解法はあまり正確ではない可能性が考えられます。
なぜなら、![]() の部分も考慮してしまっているからです。
の部分も考慮してしまっているからです。
より正確な数値を計算するなら、![]() における条件付き分布を次のように定めます。
における条件付き分布を次のように定めます。
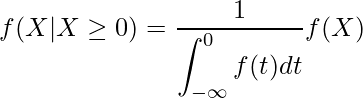
正規分布の場合には、これを特に切断正規分布と言います。
この分布について、![]() を計算すれば正しい確率が計算できます。
条件付き分布から計算した答えは次のようになります。
を計算すれば正しい確率が計算できます。
条件付き分布から計算した答えは次のようになります。
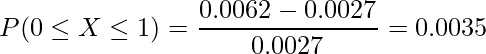
ただし、実際の試験ではここまで正確に求める必要はないと考えられます。
■問1:イ
次のように算術平均![]() を計算します。
を計算します。
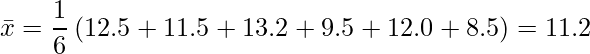
■問1:ウ
不偏分散は、次のように計算します。分母は「サンプルサイズ-1」となることに注意してください。
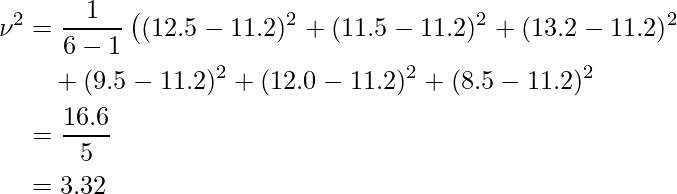
■問1:エ、オ
母分散が未知の場合における母平均の95%信頼区間は次の式で計算できます。
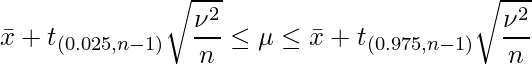
![]() は自由度bのt分布の下側aパーセント点を表します。
は自由度bのt分布の下側aパーセント点を表します。
![]() と
と![]() は、t分布表よりそれぞれ-2.571、2.571です。
数値を読み取る際は、数値表の定義をよく参照してください。
は、t分布表よりそれぞれ-2.571、2.571です。
数値を読み取る際は、数値表の定義をよく参照してください。
イ、ウの結果を代入すると、次のようになります。
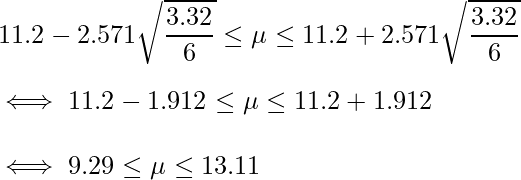
以上より、エは9.29で、オは13.11です。
■問1:カ、キ
母分散の95%信頼区間は、次の式で計算できます。
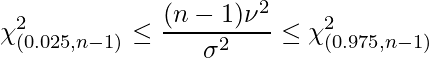
ウの結果を代入すると、次のようになります。
![]() は自由度bのカイ二乗分布の下側aパーセント点を表します。
は自由度bのカイ二乗分布の下側aパーセント点を表します。
![]() と
と![]() は、カイ二乗分布表よりそれぞれ0.83、12.83です。
数値を読み取る際は、数値表の定義をよく参照してください。
は、カイ二乗分布表よりそれぞれ0.83、12.83です。
数値を読み取る際は、数値表の定義をよく参照してください。
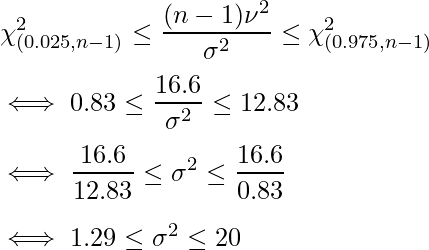
以上より、カは1.29で、キは20です。
問2
比率の信頼区間に関する問題です。問題文より、次の式が成立するような最小のnを求めればよいことが分かります。
|比率の95%信頼区間の最大値-比率の真値|≦0.03
比率の信頼区間の最大値は、次の式で計算することができます。
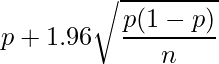
問題文から、比率の真値![]() は0.5として計算します。
これを問題文の式に代入すると、次のようになります。
は0.5として計算します。
これを問題文の式に代入すると、次のようになります。
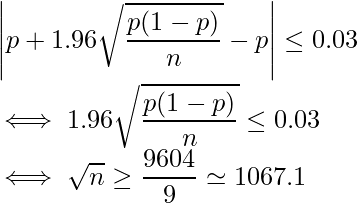
よって、nは1067.1より大きい最小の整数であることが分かります。答えは1068です。
統計学の時間で勉強しよう
今回の問題は、「統計学の時間」の記事で勉強できます。それぞれの問題について、関連する単元をリストアップしています。








