公認会計士 論文式試験の選択問題(統計学)を解く ~その2~
2017/12/05
カテゴリ:公認会計士(統計学)
概要
この記事は、平成28年公認会計士論文試験の統計学分野の選択問題(第8問)の問題2を解いたものです。 統計学の時間で一通り勉強すれば、第8問はすべて解けるようになります。
記事一覧
目次
問題2
■問1:ア
一元配置分散分析における帰無仮説は「効果はない(![]() )」です。
対立仮説は「効果がある(
)」です。
対立仮説は「効果がある(![]() )」です。
これは、「
)」です。
これは、「![]() 、
、![]() 、
、![]() 、
、![]() の中に少なくともひとつ0ではないものがある」ことを意味します。
の中に少なくともひとつ0ではないものがある」ことを意味します。
■問2
分散分析における誤差項は、重回帰分析と同じ仮定「平均0で分散が等しく、互いに独立な正規分布に従う」を満たす必要があります。
■問2:イ
誤差項は等分散、つまり分散が一定です。
■問2:ウ
誤差項は正規分布に従います。
■問2:エ
誤差項に相関はありません、つまり独立です。
■問3
因子「休憩時間」の平方和![]() と誤差の平方和
と誤差の平方和![]() を計算します。
この際、平方和の分解より「
を計算します。
この際、平方和の分解より「![]() 」が成立することを考慮すると、
」が成立することを考慮すると、![]() か
か![]() のどちらか一方を計算すればよいことが分かります。今回は、因子「休憩時間」の平方和
のどちらか一方を計算すればよいことが分かります。今回は、因子「休憩時間」の平方和![]() を計算します。
を計算します。
一元配置分散分析における因子の平方和は、次の手順で計算できます。
- ステップ1:すべての群を併合した平均値を計算する
- ステップ2:各群ごとの平均値を計算する
- ステップ3:各群ごとの群平均と全体平均を用いて平方和を計算する
- ステップ4:各群ごとの平方和の総和を計算する
では、それぞれの手順を具体的に追っていきましょう。
ステップ1
データ全体の算術平均値![]() を計算します。
を計算します。
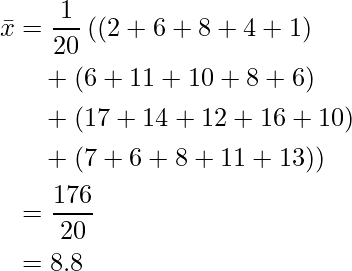
ステップ2
各群ごとの算術平均値![]() を計算します。
を計算します。
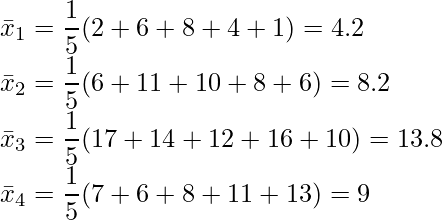
ステップ3
各群ごとに、![]() を計算します。ここで、
を計算します。ここで、![]() は各群のサンプルサイズを表します。今回は全てのiについて
は各群のサンプルサイズを表します。今回は全てのiについて![]() です。
です。
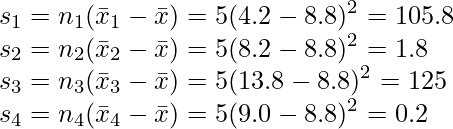
ステップ4
全ての![]() を合計します。これが求める
を合計します。これが求める![]() になります。
になります。
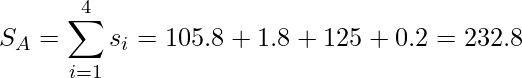
また、![]() は次のように計算できます。
は次のように計算できます。
■問4
帰無仮説を検定します。検定には、因子と誤差の平均平方![]() 、
、![]() を使用し、次のように検定統計量
を使用し、次のように検定統計量![]() を構成します。平均平方は、平方和
を構成します。平均平方は、平方和![]() を対応する自由度
を対応する自由度![]() で割ったものです。
で割ったものです。
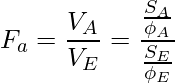
![]() の値を求めましょう。
因子の自由度
の値を求めましょう。
因子の自由度![]() は、「因子の水準数-1」で計算できます。この問題では水準数は4であるため、
は、「因子の水準数-1」で計算できます。この問題では水準数は4であるため、![]() です。
です。
誤差の自由度![]() ですが、自由度も平方和と同様に分解することができ、「
ですが、自由度も平方和と同様に分解することができ、「![]() 」の関係が成立します。
」の関係が成立します。
![]() は、「全体のサンプルサイズ-1」で計算できます。つまり。
は、「全体のサンプルサイズ-1」で計算できます。つまり。![]() です。
以上のことから、
です。
以上のことから、![]() と求められます。
と求められます。
検定統計量![]() は、
は、![]() 、
、![]() 、
、![]() 、
、![]() を用いて次のように求められます。
を用いて次のように求められます。
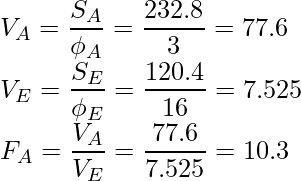
![]() は帰無仮説のもとでF分布に従うため、F検定を行います。
F分布表から、自由度(3,16)の上側5パーセント点の値を参照すればいいのですが、(3,16)の点は表に載っていません。このような場合、二通りの考え方で解くことができます。
は帰無仮説のもとでF分布に従うため、F検定を行います。
F分布表から、自由度(3,16)の上側5パーセント点の値を参照すればいいのですが、(3,16)の点は表に載っていません。このような場合、二通りの考え方で解くことができます。
- ■分布の性質を使用して解く方法
- ■自由度を補完する方法
パーセント点を固定した場合、![]() は自由度
は自由度![]() が増加すると単調に減少するため、
が増加すると単調に減少するため、
![]() の大小関係が成立します。つまり、
の大小関係が成立します。つまり、![]() が
が![]() より大きくなることはありません。
より大きくなることはありません。
これは、仮の棄却域として帰無仮説に対し保守的な値![]() を使用し検定が有意となれば、正しい棄却域
を使用し検定が有意となれば、正しい棄却域![]() を使用しても有意になることを意味します。
を使用しても有意になることを意味します。
また、検定統計量![]() は10を超えており、
は10を超えており、![]() であることも考慮すると、有意水準5%のもとでは確実に有意であると考えられます。以上より、有意水準5%で帰無仮説は棄却されます。
であることも考慮すると、有意水準5%のもとでは確実に有意であると考えられます。以上より、有意水準5%で帰無仮説は棄却されます。
分布表にない自由度でも、補完して近似値を求めることができます。調和補完による計算方法を紹介します。
2点A,Bについて、この2点を![]() に内分する点Cを計算します。
に内分する点Cを計算します。
今回は第2自由度15と20について、![]() 、
、![]() 、
、![]() と定めます。つまり次のような式で
と定めます。つまり次のような式で![]() を計算します。
を計算します。
ここで、tは次の式で計算します。
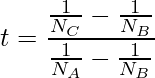
今回は![]() に第2自由度を使用します。実際に計算すると次のようになります。
に第2自由度を使用します。実際に計算すると次のようになります。
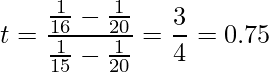
tの値が求められたので、![]() を計算しましょう。
を計算しましょう。
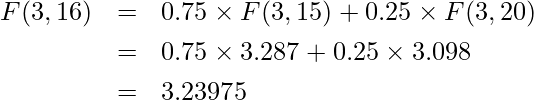
補完の結果、![]() と求められました。実際の数値は
と求められました。実際の数値は![]() であるので、精度よく補完できていることがわかります。
この値を棄却域と定め検定統計量
であるので、精度よく補完できていることがわかります。
この値を棄却域と定め検定統計量![]() と比較すればよいのですが、
と比較すればよいのですが、![]() となるため、有意となることがわかります。
となるため、有意となることがわかります。
統計学の時間で勉強しよう
今回の問題は、「統計学の時間」の記事で勉強できます。それぞれの問題について、関連する単元をリストアップしています。








