- Step1. 基礎編
- 29. 一元配置分散分析
29-4. 一元配置分散分析の流れ3
- 平均平方を求める
- 統計量Fを求める
- 統計量Fから検定を行う
平均平方は「平方和」を「自由度」で割ったもので、「要因」と「残差」のみを求めます。「要因の平均平方」は「![]() 」となります。「残差の平均平方」は「
」となります。「残差の平均平方」は「![]() 」となります。
」となります。
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 要因 | 1108.25 | 6 | 184.71 | |
| 残差 | 7976.86 | 40 | 199.42 | |
| 全体 | 9085.11 | 46 |
分散分析はこの「要因の平均平方」と「残差の平均平方」の比を用いて検定を行います。平均平方の比は、不偏分散の比と同様にF分布を用いて検定できます。
次の式から統計量Fを算出します。一元配置分散分析では要因の平均平方が「分子」、残差の平均平方が「分母」となるようにします。
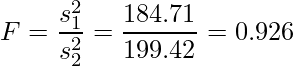
| 因 子 | 平方和 | 自由度 | 平均平方 | F 値 |
|---|---|---|---|---|
| 要因 | 1108.25 | 6 | 184.71 | 0.926 |
| 残差 | 7976.86 | 40 | 199.42 | |
| 全体 | 9085.11 | 46 |
統計量F「0.926」を、自由度(6,40)のF分布を使って検定します。分散分析では、残差のばらつき(それ以外のズレ)に対する要因のばらつき(全体の平均値からの因子の各水準の平均値のズレ)が相対的に大きいかどうかを検定します。大きい場合には要因による効果は有意であると判断されますが、小さい場合には要因による効果は有意であるとはいえません。つまり、要因のばらつきが相対的に大きいかどうかだけを見ればよいので、分散分析では必ず「片側検定」を行います。
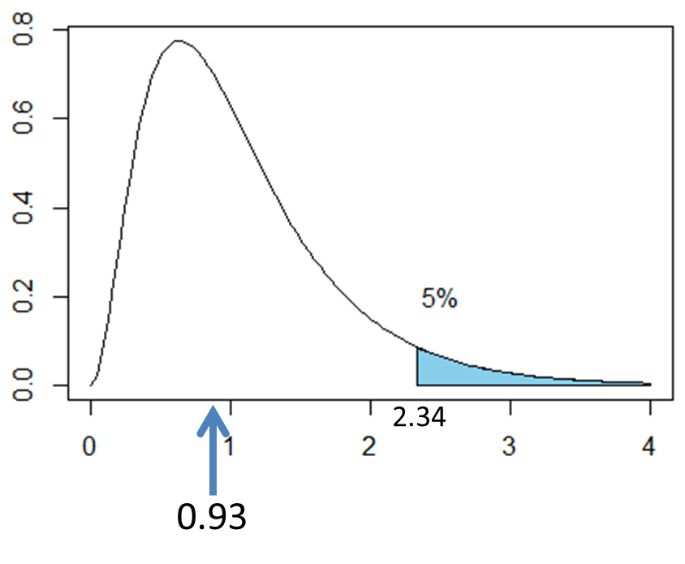
有意水準5%では、F分布表を読み取ると自由度(6, 40)のF値は「2.336」です。次の図は自由度(6,40)のF分布を表したものですが、F=0.926は図の矢印の部分に該当します。矢印は棄却域に入っていないことから、「有意水準5%の片側検定において、帰無仮説![]() は棄却さない」という結果になります。つまり、「地方によって映画館の数の母平均に差があるとはいえない」と結論づけられます。
は棄却さない」という結果になります。つまり、「地方によって映画館の数の母平均に差があるとはいえない」と結論づけられます。
■各水準の母平均の信頼区間
分散分析における各水準の母平均の信頼区間は次の式から求められます。
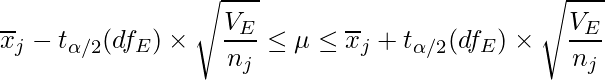
![]() は水準
は水準![]() の標本平均を、
の標本平均を、![]() は残差の自由度を、
は残差の自由度を、![]() は残差の平均平方を、
は残差の平均平方を、![]() は水準
は水準![]() におけるサンプルサイズを表します。
におけるサンプルサイズを表します。
例えば、29-2章の例題の「北海道・東北」の映画館数の母平均の95%信頼区間は
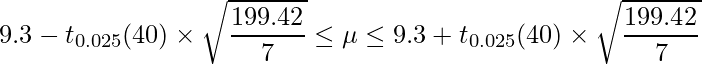
と計算できます。
29. 一元配置分散分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 28. 等分散性の検定とWelchのt検定
28-1. F分布
- 28. 等分散性の検定とWelchのt検定
28-2. F分布表
- 統計解析事例
一元配置分散分析─エクセル統計による解析事例
- ブログ
エクセル統計の分散分析について
- ブログ
Excelで重回帰分析(6) 重回帰分析の分散分析とt検定







