※コラム「統計備忘録」の記事一覧はこちら※

Excelの分析ツールを使って重回帰分析を行うと、2種類の検定結果が出力されてきます。1つは分散分析表、「母重相関係数は 0（ゼロ）である」という帰無仮説を検定しています。もう1つは偏回帰係数に続いて出力される t 検定の結果で、「偏回帰係数は 0 である」という帰無仮説を検定しています。

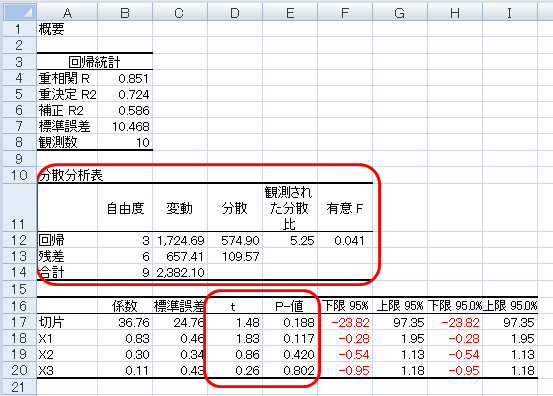
分散分析表のチェックポイントは「有意F」の値です。この値は、「回帰」と「残差」の2つの「自由度」に基づくF分布における「観測された分差比（＝F値）」の上側確率です。一般的な統計ソフトなら「ｐ値」として示されています（同じ分析ツールでも分散分析の出力では「P値」を使っています）。

有意水準を p＜0.05（5%）に設定していたのなら、この分散分析表の「有意F」は 0.041 ですから、「母重相関係数は 0 である」という帰無仮説が棄却され、「母重相関係数が 0 ではない」という対立仮説が支持されたことになります。これは、重回帰式により説明できる目的変数の変動が統計的検定によっても確認できたことを意味します。

この事例では、重相関係数が 0.851 と非常に高いのに、観測数が 10 個しかないためかろうじて有意でしたが、観測数が多くなれば、重相関係数が 0.3 未満と低い値でも有意になります。したがって、分散分析の結果が有意になったからといって安心せず、重相関係数や決定係数の値を必ず確認してください。重相関係数がどの程度あればよいかは分析の目的によって異なります。目的が予測モデルを作ることにあるのなら、重相関係数が 0.8 とか 0.9 といった高いレベルを目指すことになります。

単純にデータをコピペで2倍にしただけの重回帰分析の結果

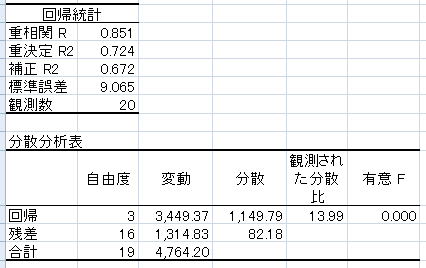
※重相関係数や決定係数の値に変化はないが分散分析の有意 F は
0.000 とかなり小さくなる。

分散分析の結果が有意になったら、次に、各説明変数の偏回帰係数の t 検定の結果を確認します。

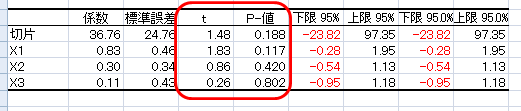
偏回帰係数のｔ検定ですが、こちらは有意になった場合、「偏回帰係数は 0 ではない」ということになります。検定統計量 ｔは「（偏回帰）係数／標準誤差」で求まります。この ｔ の値は、分散分析表の誤差の自由度による t 分布に従います。この t 値と t分布から両側確率が求められ「P-値」のところに出力されています。統計ソフトによっては、ｔ 値の代わりに F 値が出力されているものがありますが、ｔ² ＝ F という関係にあり、どちらでも確率は同じです。

この検定は「偏回帰係数が 0 ではない」を対立仮説とする両側検定の結果ですが、対立仮説が、「偏回帰係数が 0 より大きい」あるいは「偏回帰係数が 0 より小さい」なら片側検定になりますから、その場合は「P-値」を2で割ってください。

「P-値」の右側には「下限 95％」、「上限 95%」の出力があります。これは、偏回帰係数の信頼区間です。「P-値」が 0.05 以上なら信頼区間の限界値は 0 を挟んだ値になります。説明変数の影響がプラス、マイナスのどちらもありうるということです。今回の事例では、どの説明変数の偏回帰係数も 0.05 以上なので、すべての信頼区間が 0 を含んでいます。

偏回帰係数が有意ということは、その説明変数の目的変数に対する影響力が統計的にも確認できたということです。ただし、この影響力を絶対的なものと考えるのは誤りです。説明変数の組み合わせを変えれば、偏回帰係数は変化してしまいます。目的変数との関係が第3の変数を介した間接的なものであったり、交絡因子が存在したりという場合です。新たな変数を加えて重回帰分析をし直したら、影響力が消えてしまった、偏回帰係数の符号が逆転したということは珍しくありません。

第3の変数の影響については、また別の機会に触れたいと思います。