※コラム「統計備忘録」の記事一覧はこちら※

今回は、「重相関係数と決定係数」からの続きです。

さて、分析ツールによる回帰分析の「回帰統計」の出力欄には、重相関係数と決定係数のほかに、「補正 R2」と「標準誤差」というのがあります。

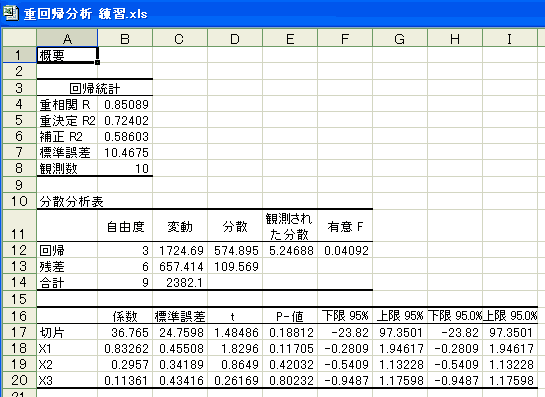
「補正 R2」は、一般に「自由度調整済み決定係数」あるいは「自由度修正済み決定係数」と呼ばれるものです。次の式によって求まります。式の中の p は説明変数の数です。

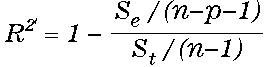
重回帰分析で説明変数を増やしていくと決定係数は次第に 1 に近づいていきます。例えば同じサンプルのデータで、説明変数が 3個と 4個の 2通りの重回帰分析を行った場合、説明変数を 4個にした方が決定係数は高くなります。決定係数が高くなったのが説明変数の数を増やしただけの効果によるものか、増やした以上の効果があったのかを見たいとき、この自由度調整済み決定係数を比較します。説明変数を増やした場合の調整済み決定係数の方が高ければ、説明変数を増やしたことにより重回帰式の精度が良くなったと評価できます。

自由度調整済みの決定係数（ R²' ）と調整していない決定係数（ R² ）を比較すると、調整済み決定係数の方が小さくなります。また、n が小さなサンプルでは 2つの値の差が大きくなります。先ほどの式を次のように展開してみると理由が良く分かります。

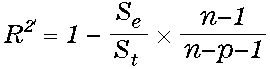
次に「標準誤差」ですが、これは分散分析表の「残差の分散」の二乗根です。Excelに次の式を入力して確認してみてください。

＝SQRT(残差の分散)

残差は観測値と重回帰式による推定値の差です。標準誤差が「残差の分散の二乗根」ということは、すなわち「残差の標準偏差」ということになります。この値をみれば、重回帰式による推定値からどの程度の範囲に観測値が散らばっているのか見積もることができます。