- Step1. 基礎編
- 29. 一元配置分散分析
29-2. 一元配置分散分析の流れ1
分散分析のポイントは「データ全体の平均値から因子の各水準の平均値がどのくらいずれているか」を見ることです。そのため、「データ全体の平均値からの各データのズレ」を「データ全体の平均値からの因子の各水準の平均値のズレ」と「それ以外のズレ(因子の各水準の平均値からの各データのズレ)」の3つに分けて考えます。
■分散分析のイメージ
このデータの全体の平均は「18」です。A、B、C群の平均はそれぞれ「20」、「16」、「18」です。
| A群 | 10 | 20 | 30 |
|---|---|---|---|
| B群 | 14 | 16 | 18 |
| C群 | 20 | 12 | 22 |
・全体の平均値からの各データのズレ
| A群 | 18-10=8 | 18-20=-2 | 18-30=-12 |
|---|---|---|---|
| B群 | 18-14=4 | 18-16=2 | 18-18=0 |
| C群 | 18-20=-2 | 18-12=6 | 18-22=-4 |
・全体の平均値からの因子の各水準の平均値のズレ
| A群 | 18-20=-2 | 18-20=-2 | 18-20=-2 |
|---|---|---|---|
| B群 | 18-16=2 | 18-16=2 | 18-16=2 |
| C群 | 18-18=0 | 18-18=0 | 18-18=0 |
・それ以外のズレ(因子の各水準の平均値から各データのズレ)
| A群 | 20-10=10 | 20-20=0 | 20-30=-10 |
|---|---|---|---|
| B群 | 16-14=2 | 16-16=0 | 16-18=-2 |
| C群 | 18-20=-2 | 18-12=6 | 18-22=-4 |
これらの3つのズレを式にすると次のようになります。ズレは2乗和として求めます。
「全体の平均値からの各データのズレ」=「全体の平均値からの因子の各水準の平均値のズレ」+「それ以外のズレ」
例題:
下の表は都道府県内にある映画館の数を地方ごとに分けた表です。このデータから、地方によって映画館の数の母平均に差があるかを検定します。帰無仮説![]() は「各地方の映画館数の母平均は等しい」とします。
は「各地方の映画館数の母平均は等しい」とします。
| 北海道・東北 | 21 | 12 | 8 | 11 | 6 | 3 | 4 | ||
|---|---|---|---|---|---|---|---|---|---|
| 関東 | 92 | 15 | 6 | 5 | 5 | 5 | 5 | ||
| 中部 | 2 | 18 | 5 | 5 | 21 | 6 | 0 | 2 | 14 |
| 近畿 | 8 | 20 | 11 | 34 | 4 | 0 | 10 | ||
| 中国 | 8 | 13 | 5 | 0 | 1 | ||||
| 四国 | 2 | 3 | 3 | 1 | |||||
| 九州・沖縄 | 13 | 2 | 2 | 5 | 5 | 9 | 4 | 7 |
出典:一般社団法人日本映画製作者連盟(2015年12月末現在)
- 「データ全体の平均値」と「各群(地方)の平均値」を求める
- 「データ全体の平均値からの各データのズレ」を求める
- 「データ全体の平均値からの因子の各水準の平均値のズレ」を求める
- 「それ以外のズレ」を求める
データ全体の平均値は「9.38」、各群(地方)の平均値は次のようになります。
| 北海道・東北 | 9.29 |
|---|---|
| 関東 | 19.00 |
| 中部 | 8.11 |
| 近畿 | 12.43 |
| 中国 | 5.40 |
| 四国 | 2.25 |
| 九州・沖縄 | 5.88 |
全体の平均値と47都道府県すべてのデータとの差の二乗和を求めます。
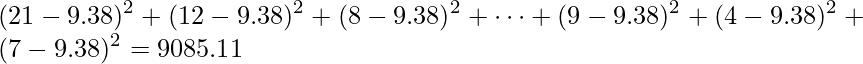
全体の平均値と7地方それぞれにおける平均値との差を二乗したものに、各地方に含まれるデータ数(都道府県数)をかけたものの和を求めます。
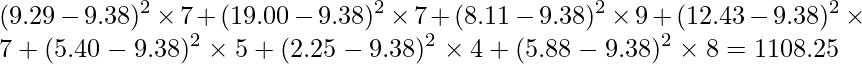
「それ以外のズレ」=「全体の平均値からの各データのズレ」-「全体の平均値からの因子の各水準の平均値のズレ」なので、「![]() 」となります。
」となります。
ここまでで、一元配置分散分析の第一段階は完了です。
29. 一元配置分散分析
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 6. 分散と標準偏差
6-1. 分散
- 23. 検定の前に
23-2. 検定で使う用語
- 統計解析事例
一元配置分散分析─エクセル統計による解析事例
- ブログ
エクセル統計の分散分析について
- ブログ
Excelで重回帰分析(6) 重回帰分析の分散分析とt検定







