一元配置分散分析─エクセル統計による解析事例

2017/04/19

※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

分析データ

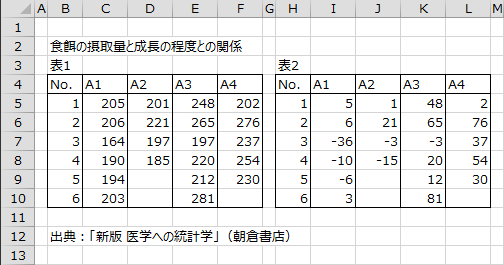
食餌の摂取量と成長の程度との関係を調べるために、4種の食餌摂取量で24匹のネズミに無作為に餌付けたところ、12週間後の成長を示すパラメーターが下図表1のように得られました。水準A2では2匹、A4では1匹のデータが得られていません。表2は表1の値から200を引いた値で、こちらを分析に用います。（出典；「医学への統計学［第3版］」朝倉書店）

分析の目的

食餌の摂取量の違いによって成長の程度に有意差が認められるかを調べます。また、各水準間での成長の程度の違いについても調べます。

データラベルの選択

下図のように表の先頭行「I4:L4」を選択します。

メニューの選択

メニューより［エクセル統計］→［分散分析・多重比較］→［一元配置分散分析］を選択します。表のセル範囲「I4:L10」が［データ入力範囲］に指定された状態でダイアログが表示されます。「多重比較（すべての対比較）」の［Tukey-Kramer］にチェックを入れて［OK］ボタンをクリックします。

出力内容

出力内容のリストがハイパーリンク付きで出力されます。

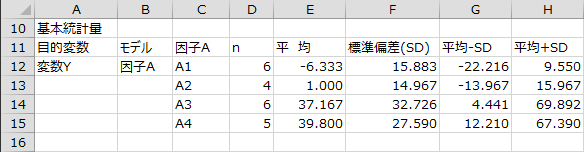
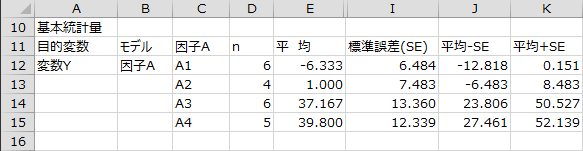
基本統計量

基本統計量として、サンプルサイズ、平均、標準偏差（SD）、平均－SD、平均＋SD、標準誤差（SE）、平均?SE、平均＋SDが出力されます。

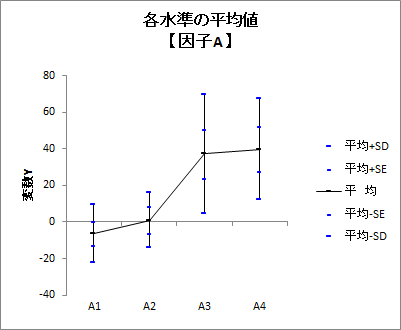
各水準の平均値グラフ

各水準の平均値の折れ線グラフが出力されます。

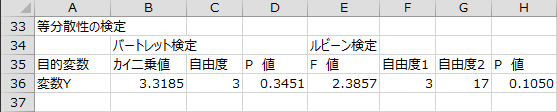
等分散性の検定

等分散性の検定として、バートレット検定とルビーン検定の結果が出力されます。

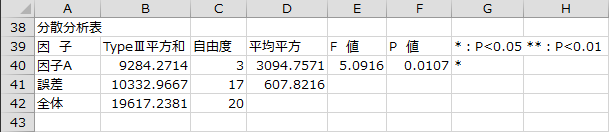
分散分析表

分散分析表として各因子の平方和、自由度、平均平方、F値、P値、判定結果が出力されます。

等分散性を仮定しない検定

グループ間での等分散性が仮定されない場合の修正分散分析として、F値、自由度、P値、判定結果が出力されます。

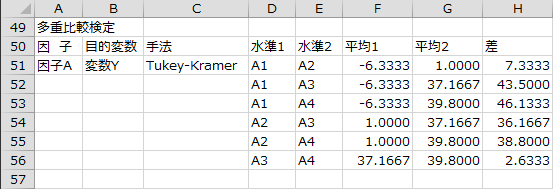
多重比較検定

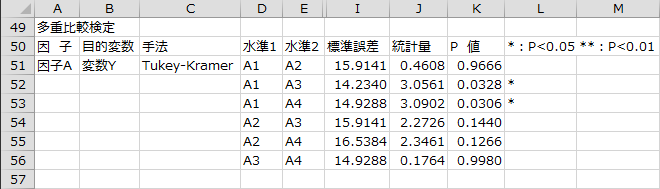
Tukey-Kramerの方法による多重比較の結果が出力されます。

考察

等分散性の検定の結果、バートレット検定ではP値が0.3451、ルビーン検定ではP値が0.1050なので、いずれも有意水準5%で帰無仮説「各水準の母分散は等しい」は棄却されませんでした。

分散分析の結果、P値が0.0107なので、有意水準5%で食餌摂取量による成長の程度に有意差があると言えます。

多重比較検定の結果、有意水準5%でA1とA3、A1とA4で母平均は等しいとは言えません。

※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_21.xlsx

このファイルは、エクセル統計の体験版に対応しています。

ブログ