公認会計士 論文式試験の選択問題(統計学)を解く ~その3~
2017/12/06
カテゴリ:公認会計士(統計学)
概要
この記事は、平成28年公認会計士論文試験の統計学分野の選択問題(第8問)の問題3を解いたものです。 統計学の時間で一通り勉強すれば、第8問はすべて解けるようになります。
記事一覧
目次
問題3
■問1
単回帰分析において、説明変数と目的変数の相関係数![]() と決定係数
と決定係数![]() の間には「
の間には「![]() 」の関係が成立します。
つまり、相関係数の絶対値は決定係数の正の平方根に一致します。
」の関係が成立します。
つまり、相関係数の絶対値は決定係数の正の平方根に一致します。
ただし符号はやや注意する必要があり、回帰係数の符号と一致することを覚えておきましょう。
この事実は、単回帰分析の回帰係数と相関係数の式を見比べると理解できます。まず、回帰係数の推定量![]() は次の通りです。
は次の通りです。
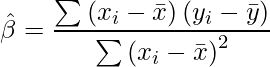
次に相関係数![]() の式を確認しましょう。
の式を確認しましょう。
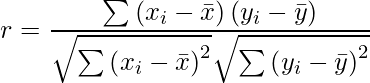
どちらも分子は共通で、共分散をn倍したものであることが分かります。一方で、分母は2乗の形になっているため常に正の値をとります。これはつまり、![]() と
と![]() の符号は常に一致することを意味します。
の符号は常に一致することを意味します。
さて、この問題では回帰係数は正の値であることから、![]() で計算できることが分かります。
以上の事から、
で計算できることが分かります。
以上の事から、![]() と求められます。
と求められます。
■問2
予測値は、条件付き期待値![]() です。と言っても、回帰式に特定の
です。と言っても、回帰式に特定の![]() を代入するだけで計算できます。第2階級の消費支出は228010ですから、予測値
を代入するだけで計算できます。第2階級の消費支出は228010ですから、予測値![]() は次のように計算できます。
は次のように計算できます。
次に残差です。残差の定義は「真の値と予測値の差」ですから、次のように計算できます。
■問3
最小二乗法で回帰分析を行った場合、残差の合計は0となります。ただしこの問題では数値が丸められているため、実際に計算すると0にはなりません。
■問4
偏回帰係数は、t型の統計量で検定できます。偏回帰係数の推定値を![]() 、偏回帰係数の標準誤差を
、偏回帰係数の標準誤差を![]() 、回帰式に含まれる説明変数の数を
、回帰式に含まれる説明変数の数を![]() とおくと、検定統計量とその分布は次のようになります。
とおくと、検定統計量とその分布は次のようになります。
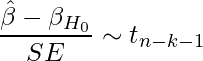
単回帰式の場合は![]() であるため、自由度8のt分布を用いて検定できることが分かります。
であるため、自由度8のt分布を用いて検定できることが分かります。
![]() は帰無仮説のもとでの
は帰無仮説のもとでの![]() の値で、問題文より
の値で、問題文より![]() です。
それぞれ値を代入して検定統計量を求めると、次のようになります。
です。
それぞれ値を代入して検定統計量を求めると、次のようになります。
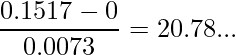
対立仮説は![]() であるため、片側検定となることに注意しましょう。
t分布表から自由度8のt分布の5%点を読み取ると、棄却点は1.860です。
であるため、片側検定となることに注意しましょう。
t分布表から自由度8のt分布の5%点を読み取ると、棄却点は1.860です。
![]() であるため、帰無仮説は棄却されます。
であるため、帰無仮説は棄却されます。
■問5
単回帰分析において、回帰係数は「1単位変化した際の目的変数の変化量」を意味します。 一方、重回帰分析においては、「その他の変数が固定されている時に、その説明変数が1単位変化した際の目的変数の変化量」を表します。
単回帰分析ではその他の説明変数が存在しないため、「その他の変数が固定されている際に」という部分が不要になります。 別の表現として「他の変数の影響を調整した」等が挙げられます。
重回帰分析において説明変数間に相関がある場合、モデルに変数を追加するとどのような変化が起こるかを確認しましょう。 以下は、3つのモデルについて、エクセル統計で計算した結果です。
- モデル1:食料費 = 消費支出
- モデル2:食料費 = 消費支出 + 世帯人員
- モデル3:食料費 = 世帯人員
食料費 = 22847 + 0.1517 × 消費支出
食料費 = -19250 + 1.1347 × 消費支出 + 13979 × 世帯人員
食料費 = -178913 + 73624 × 消費支出
モデル1とモデル2は問題でも提示されているモデルです。 モデル1に世帯人員を説明変数として加えるとモデル2になります。 このとき、消費支出の偏回帰係数の推定値が減少していることが分かります。
モデル3を見てみましょう。 これは説明変数として世帯人員だけを使用しているモデルです。 偏回帰係数は73624です。 モデル3に消費支出を説明変数として加えるとモデル2になります。 このとき、世帯人員の偏回帰係数の推定値はモデル3に比べて19250まで低下しています。
このように説明変数が相関を持つ場合は、モデルに説明変数を追加あるいは除去することによって偏回帰係数が変化します。 今回の場合、説明変数間だけでなく、説明変数と目的変数間にも正の相関があるため、同時に説明変数として使用すると互いの影響が調整されます。その結果、偏回帰係数の値が変化したと考えられます。統計学の時間で勉強しよう
今回の問題は、「統計学の時間」の記事で勉強できます。それぞれの問題について、関連する単元をリストアップしています。
- 問題3







