移動平均の計算方法
2017/12/13
カテゴリ：Tips
移動平均の計算方法を紹介します。
概要
移動平均とは、時系列データにおいて、ある一定区間ごとの平均値を区間をずらしながら求めたものです。移動平均を用いてグラフを作成すると、長期的な傾向を表す滑らかな曲線が得られます。移動平均の計算方法は区間が奇数か偶数かによって異なります。
区間が奇数の場合
区間を2n＋1（n≥1）とすると、第a期（a≥n+1）の移動平均値は、第a−n期から第a＋n期の平均値となります。例えば、区間が3の場合の第9期の移動平均値は、第8期から第10期（8・9・10）の平均値となります。
は
期のデータを、
は
期の移動平均とおくと、移動平均の計算式は次のように表せます。
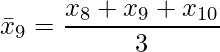
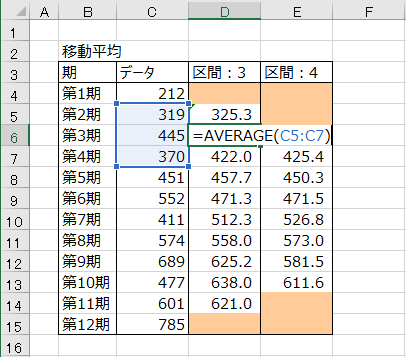
下図では、第1期から第12期までのデータに対し、区間3で第2期から第11期までの移動平均を求めたものです。
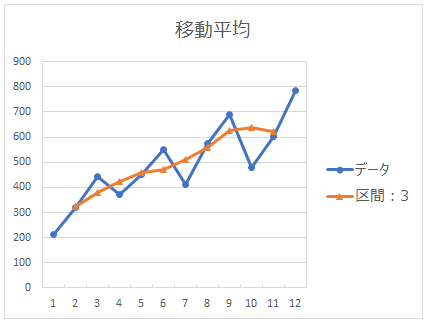
グラフに表すと下図のようになります。
区間が偶数の場合
区間を2n（n≥1）とすると、第a期（a≥n+1）の移動平均値は、第a−n期から第a＋n−1期の平均値と第a−n＋1期から第a＋n期の平均値の平均となります。例えば、区間が4の場合の第9期の移動平均値は、第7期から第10期（7・8・9・10）の平均値と第8期から第11期（8・9・10・11）の平均値の平均になります。式で表すと次のようになります。
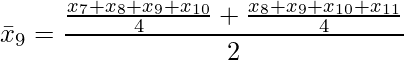
下図では、第1期から第12期までのデータに対し、区間4で第3期から第10期までの移動平均を求めたものです。
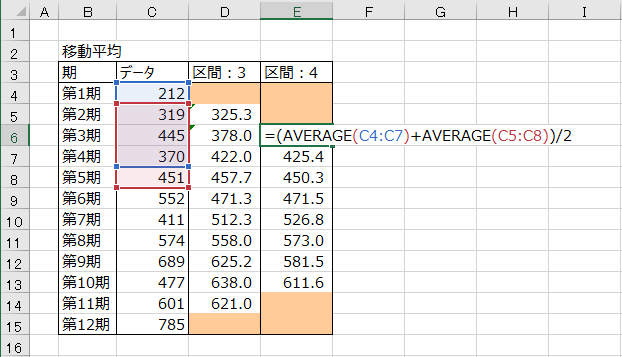
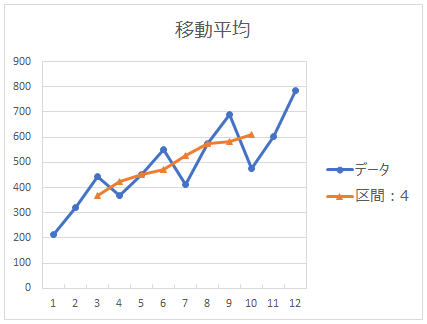
グラフに表すと下図のようになります。
移動平均の意味
時系列データの周期と移動平均の区間が等しい場合、周期の影響は完全に排除されます。次のデータは、Y=2Xという線形トレンドに周期3の変動を加えて作った人工的な時系列データです。この時系列データについて区間3の移動平均を計算すると、周期が除去されて、元の線形トレンドに戻ります。
ただし、実際のデータでは複数の周期性や不規則変動が含まれるため、移動平均によって周期の影響を完全に除去することはできません。
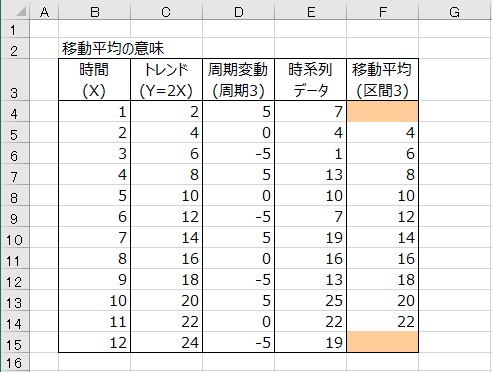
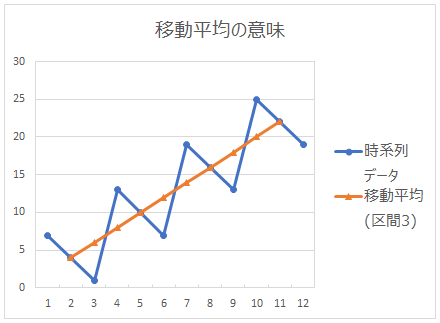
下図は上記のデータをグラフに表したものです。移動平均では時系列データの周期性が除去されているのがわかります。
ダウンロード
この統計TipのExcel ファイルのダウンロードはこちらから → tips_12.xlsx
このコンテンツは、Excel 2016を用いて作成しています。
