統計検定2級CBT公式問題集の解説(確率分布の分野)
2023/08/12
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問1:確率分布の定数の決定に関する問題
- 問2:正規確率の計算に関する問題
- 問3:確率変数の関数の期待値に関する問題
- 問4:2項分布の正規近似に関する問題
- 問5:2項確率の比に関する問題
- 問6:分布形と歪度・尖度に関する問題
- 問7:X-Yの確率計算に関する問題
- 問8:線形な変数変換、共分散、相関係数に関する問題
問1
確率密度関数は、連続型確率変数 ![]() に対して確率を得るための関数を
に対して確率を得るための関数を ![]() で表したもので、次の式が成り立ちます。
で表したもので、次の式が成り立ちます。
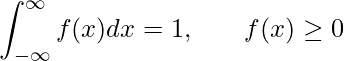
また、![]() が
が ![]() から
から ![]() までの値を取るとき、その確率は次のように計算できます。
までの値を取るとき、その確率は次のように計算できます。
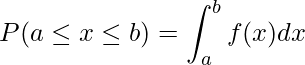
問題文の確率密度関数に対して1つ目の式を用いると、
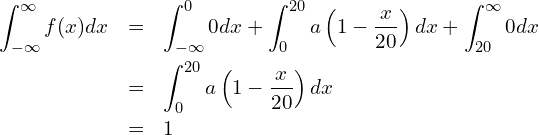
となります。この式を整理すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle \int_{0}^{20} a\left(1-\frac{x}{20} \right)dx &=& a \left[x-\frac{1}{2} \times \frac{x^2}{20}\right]^{20}_0 \\ &=& a \left[x-\frac{x^2}{40}\right]^{20}_0 \\ &=& a(20-10) \\ &=& 10a \\ &=& 1 \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-bbc49f5999958a49d2affe58350fdc32_l3.png)
となります。これを解くと、![]() となります。
となります。
問2
まず、-1と4を標準化します。ある確率変数 ![]() が平均
が平均 ![]() 、分散
、分散 ![]() の正規分布に従う時、
の正規分布に従う時、![]() から平均
から平均 ![]() を引いて
を引いて ![]() で割った値を
で割った値を ![]() とおくと、この
とおくと、この ![]() は「平均が0、分散が1の標準正規分布」に従います。標準化を行うことにより、単位や平均値などが異なるデータ同士の大小を「標準正規分布表」を使って比較できるようになります。
は「平均が0、分散が1の標準正規分布」に従います。標準化を行うことにより、単位や平均値などが異なるデータ同士の大小を「標準正規分布表」を使って比較できるようになります。
−1を標準化すると
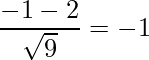
となります。4を標準化すると
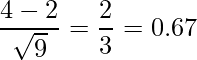
となります。これらの結果から、
となります。
![]() であることから、標準正規分布表より
であることから、標準正規分布表より ![]() となる確率は0.16であり、
となる確率は0.16であり、![]() となります。
となります。
また、標準正規分布表より ![]() となる確率は0.25です。
となる確率は0.25です。
したがって、![]() となります。
となります。
データの標準化の詳細については「14-3. 標準化したデータの使い方」をご覧ください。
問3
確率密度関数 ![]() から期待値
から期待値 ![]() を計算する場合には、次の式を使います。
を計算する場合には、次の式を使います。
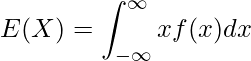
問題文の値を用いて計算すると
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E(X) &=& \int_{-\infty}^{\infty} xf(x)dx \\ &=&\int_{0}^{10} 1000 \times \frac{1}{10}\left(1-\frac{x}{20} \right) dx + \int_{10}^{15} 1120 \times \frac{1}{10}\left(1-\frac{x}{20} \right) dx \\ &+& \int_{15}^{20} 1280 \times \frac{1}{10}\left(1-\frac{x}{20} \right) dx \\ &=&\int_{0}^{10} 100 \times \left(1-\frac{x}{20} \right) dx + \int_{10}^{15} 112 \times \left(1-\frac{x}{20} \right) dx \\ &+& \int_{15}^{20} 128 \times \left(1-\frac{x}{20} \right) dx \\ &=& \left[100 \times \left(x-\frac{x^2}{40} \right)\right]^{10}_{0} + \left[112 \times \left(x-\frac{x^2}{40}\right) \right]^{15}_{10} \\ &+& \left[128 \times \left(x-\frac{x^2}{40}\right) \right]^{20}_{15} \\ &=& 100 \times (10-2.5) + 112 \times (15-5.6-(10-2.5)) \\ &+& 128 \times (20-10-(15-5.6)) \\ &=& 750 + 212.8 + 76.8 \\ &=& 1040 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-fe44a9efc736ca0bfa0fa7b7aed91548_l3.png)
となります。
確率密度関数の期待値の詳細については「12-3. 確率変数の期待値」をご覧ください。
問4
成功確率が ![]() である試行を
である試行を ![]() 回行うときに成功する回数
回行うときに成功する回数 ![]() が従う確率分布である二項分布では、
が従う確率分布である二項分布では、![]() が十分に大きい場合には、次の式から得られる
が十分に大きい場合には、次の式から得られる ![]() が標準正規分布に従います。
が標準正規分布に従います。![]() は標本比率を表します。
は標本比率を表します。
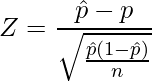
問題文の値を使うと
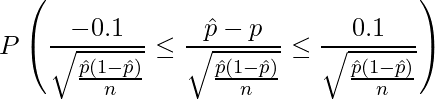
となります。問題文より、
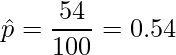
であることから、
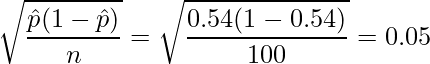
となります。この値を使うと、
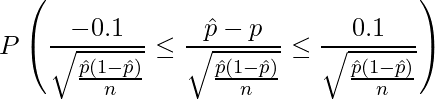
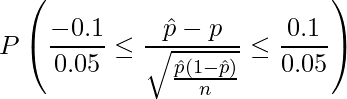
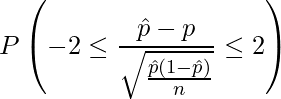
標準正規分布表より ![]() となる確率は0.0228であることから、求める確率は
となる確率は0.0228であることから、求める確率は![]() となります。
となります。
二項分布の正規近似の詳細については「21-1. 母比率の信頼区間の求め方1」をご覧ください。
問5
![]() 回のベルヌーイ試行を行うときに成功する回数
回のベルヌーイ試行を行うときに成功する回数 ![]() がちょうど
がちょうど ![]() 回となる確率、すなわち
回となる確率、すなわち ![]() となる確率は次の式から計算することができます。
となる確率は次の式から計算することができます。
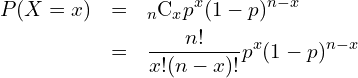
一方、 ![]() となる確率は次の式から計算することができます。
となる確率は次の式から計算することができます。
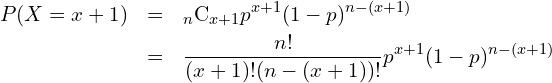
したがって、
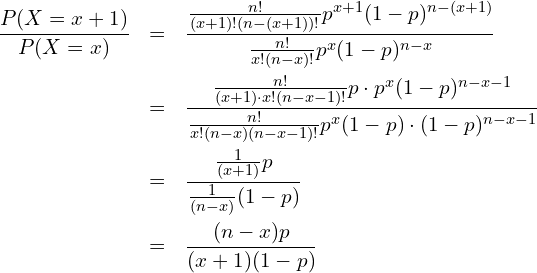
問題文より、![]() 、
、![]() であることから
であることから
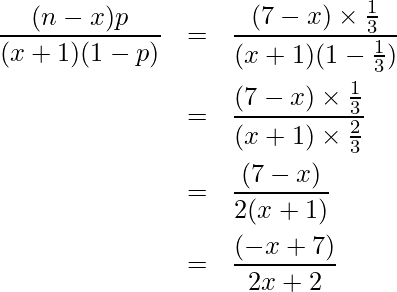
となります。
二項分布の詳細については「13-1. 二項分布」をご覧ください。
問6
I:× 歪度は、「右裾が長い」もしくは「右に歪んだ」もしくは「左に偏った」分布のときには正の値を、「左裾が長い」もしくは「左に歪んだ」もしくは「右に偏った」分布のときには負の値をとります。
II:× 尖度は、正規分布より尖った分布(データが平均付近に集中し、分布の裾が重い)のときには正の値を、正規分布より扁平な分布(データが平均付近から散らばり、分布の裾が軽い)のときには負の値をとります。
III:× t分布は自由度が大きくなるほど正規分布に近づきます。正規分布の場合には尖度0になることから、t分布の自由度が大きくなるほど尖度の絶対値は小さくなります。
歪度と尖度の詳細については「3-5. 歪度と尖度」をご覧ください。
問7
ある年の6月における電気料金 ![]() と前年の6月における電気料金
と前年の6月における電気料金 ![]() との差を考えます。
との差を考えます。![]() および
および ![]() はそれぞれ独立で同一の正規分布で近似されます。したがって、
はそれぞれ独立で同一の正規分布で近似されます。したがって、
問題文より、
となります。求める確率は ![]() です。標準化を行うと
です。標準化を行うと
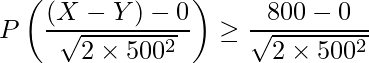
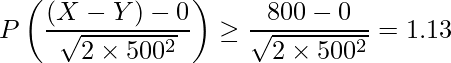
標準正規分布表を見ると、 ![]() となる確率は0.129です。したがって、
となる確率は0.129です。したがって、![]() となる確率は0.129となります。
となる確率は0.129となります。
2変数の期待値と分散の詳細については「15-6. 2変数の期待値と分散」をご覧ください。
問8
2つの確率変数 ![]() と
と ![]() の共分散
の共分散 ![]() と相関係数
と相関係数 ![]() は次の式から計算できます。
は次の式から計算できます。
![Rendered by QuickLaTeX.com \displaystyle r_{XY} = \frac{Cov(X,Y)}{\sqrt{V[X]V[Y]}}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-3e9b56e78474ef587371136d7c284285_l3.png)
問題文の値を用いて計算すると
![Rendered by QuickLaTeX.com \displaystyle r_{XY} = \frac{Cov(X,Y)}{\sqrt{V[X]V[Y]}} = \frac{0.3}{\sqrt{1.0 \times 1.0}} = 0.3](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-f9bf4768be4f9b07023a6515fa34cf96_l3.png)
となります。次に、![]() と
と ![]() について期待値、分散を計算します。
について期待値、分散を計算します。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle E[UV] &=& E[(3X-2)(-2Y-4)] \\ &=& E[-6XY-12X+4Y+8] \\ &=& -6E[XY] -12E[X] + 4[Y] + E[8] \\ &=& -6 \times 6.3 -12 \times 2.0 + 4 \times 3.0 + 8 \\ &=& -41.8 \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-9bf77a77ee8e8c6f64e5b5b82e1d748c_l3.png)
したがってこれらの値を用いると、共分散 ![]() 、相関係数
、相関係数 ![]() は
は
![Rendered by QuickLaTeX.com \displaystyle r_{UV} = \frac{Cov(U,V)}{\sqrt{V[U]V[V]}} = \frac{-1.8}{\sqrt{9 \times 4}} = \fraq{-1.8}{6} = -0.3](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-099c7b4f9429d252fd128f9701fc1082_l3.png)
となります。
2変数の期待値と分散の詳細については「15-6. 2変数の期待値と分散」をご覧ください。








