2021年6月統計検定2級の問題の解説(その2)
2021/08/07
カテゴリ:統計検定
タグ:2021年6月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問8:同時確率関数に関する問題
- 問9:確率の計算に関する問題
- 問10:正規分布と正規化に関する問題
- 問11:確率変数と累積分布関数に関する問題
- 問12:幾何分布に関する問題
- 問13:推定量の算出に関する問題
- 問14:推定量の不偏性と分散に関する問題
問8 [10]
与えられた同時確率関数から、1つ1つの確率を求めます。
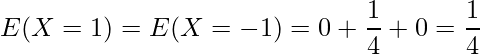
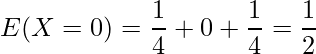
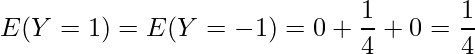
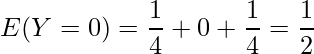
したがって、これらの確率を用いて、
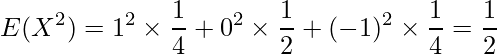
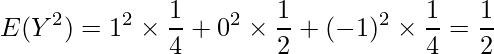
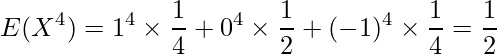
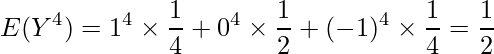
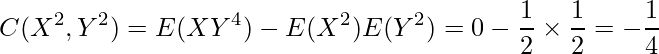
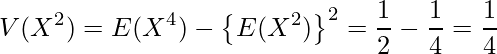
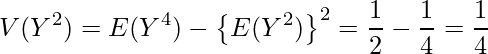
となります。したがって、相関係数は
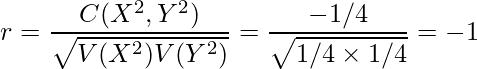
となります。また、![]() と
と![]() が独立であるかどうかを確認するために
が独立であるかどうかを確認するために![]() が成り立つかどうかを確認します。
が成り立つかどうかを確認します。![]() 、
、![]() のとき
のとき![]() 、
、![]() 、
、![]() であり、
であり、![]() が成り立ちません。したがって、
が成り立ちません。したがって、![]() と
と![]() は互いに独立ではありません。
は互いに独立ではありません。
※このようにガリガリ計算すると相関係数が計算ができるのですが、試験時間を考えるとあまり得策ではないかもしれません。高速で答えを導くにはまず![]() と
と![]() が0及び1のときの確率を求めます。与えられた同時確率関数から
が0及び1のときの確率を求めます。与えられた同時確率関数から
![]() 、
、![]() 、
、![]() 、
、![]()
となることから、相関係数は-1と分かります。
問9 [11]
25人全員がバラバラの誕生日である確率は
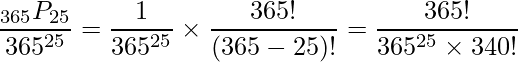
となります。分子の![]() は「365日の中から重複を許さず25日を選んで並べる」場合の数を意味します。
は「365日の中から重複を許さず25日を選んで並べる」場合の数を意味します。
したがって、25人の中で同じ誕生日の人が存在する確率は
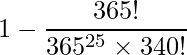
となります。
問10 [12]
まず、標準正規分布表の中から「0.011」を探します。すると、![]() であることが分かります。これは
であることが分かります。これは![]() と表すこともできます。
と表すこともできます。
次に、標準正規分布上の![]() を正規分布
を正規分布![]() 上の値に変換します。正規分布
上の値に変換します。正規分布![]() に従う値
に従う値![]() を正規化(標準正規分布上の値に変換)するには、
を正規化(標準正規分布上の値に変換)するには、![]() から平均
から平均![]() を引き、その値を標準偏差
を引き、その値を標準偏差![]() で割ります。ここで、求める値を
で割ります。ここで、求める値を![]() とおくと、
とおくと、
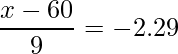
より、![]() となります。
となります。
問11 [13]
累積分布関数とは「確率変数![]() がある値
がある値![]() 以下(
以下(![]() )の値となる確率」を表す関数です。問題文より
)の値となる確率」を表す関数です。問題文より![]() が1以下となる確率は1であることから、
が1以下となる確率は1であることから、![]() が1より大きくなる確率は0となります。
が1より大きくなる確率は0となります。
問11 [14]
まずは、累積分布関数![]() から確率密度関数
から確率密度関数![]() を求めます。確率密度関数は累積分布関数を微分することで求めることができます。
を求めます。確率密度関数は累積分布関数を微分することで求めることができます。
![]() と
と![]() は定数なので微分すると0になることから、ここでは
は定数なので微分すると0になることから、ここでは![]() の範囲のみを考えます。
の範囲のみを考えます。![]() を微分すると
を微分すると![]() になります。
になります。
確率密度関数の期待値は次の式から求められます。
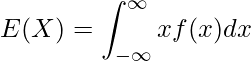
したがって、求める期待値は
![Rendered by QuickLaTeX.com \displaystyle E(X)=\int^{\infty}_{-\infty}xf(x)dx=\int^{1}_{0}x \times 1 dx=\int^{1}_{0}xdx=\left[\frac{1}{2}x^2\right]^1_0=\frac{1}{2}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b8c21c634976a8282c7ec926ccc29a24_l3.png)
となります。
問12 [15]
確率変数![]() が成功確率
が成功確率![]() の幾何分布に従っている時、期待値は以下のようになります。
の幾何分布に従っている時、期待値は以下のようになります。
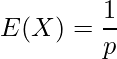
問題文より![]() なので、求める期待値は
なので、求める期待値は
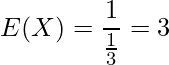
となります。幾何分布の詳細についてはこちらをご覧ください。
問12 [16]
確率変数![]() における期待値
における期待値![]() と分散
と分散![]() 、任意の値を
、任意の値を![]() とすると、チェビシェフの不等式は次のように表せます。
とすると、チェビシェフの不等式は次のように表せます。
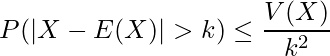
ただし、この問題は標本平均に関する問題なので、
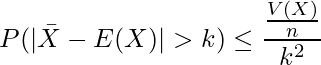
となります。問題文より、分散は
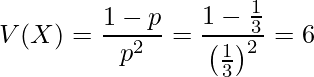
となります。したがってチェビシェフの不等式は次のように書けます。
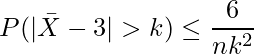
問13 [17]
I:○ 推定量は一意に定まる値ではなく、様々な値を取ります。そして、それらの値を取る確率が決まっているので、確率変数です。
II:○ 一致性の定義より正しいです。
III:× 「一致性」と「不偏性」は全く異なる性質を表す指標です。
問14 [18]
標本から算出した推定量の期待値が母集団のそれに等しいとき、その推定量を不偏推定量と言います。与えられた式の期待値を1つずつ求めてみます。
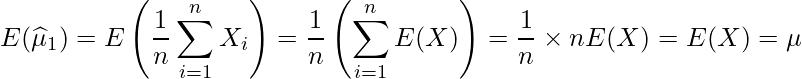
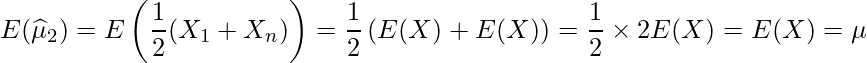
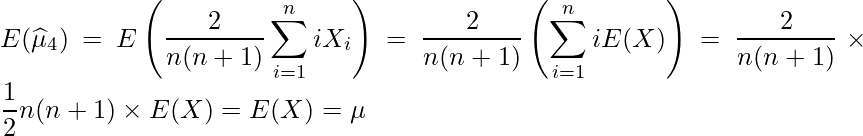
したがって、![]() 、
、![]() 、
、![]() 、
、![]() はすべて
はすべて![]() の不偏推定量であることが分かります。
の不偏推定量であることが分かります。
問14 [19]
与えられた式の分散を1つずつ求めてみます。
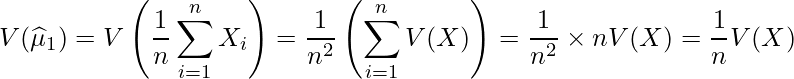
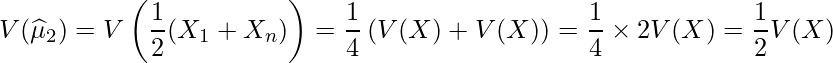
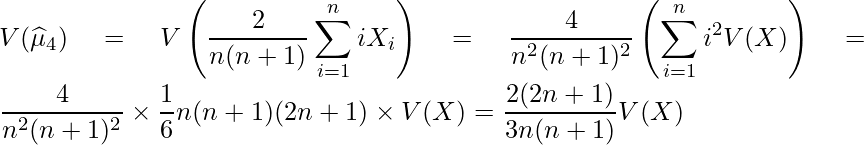
![]() の係数を比較すると、
の係数を比較すると、![]() であり、
であり、![]() であることから、
であることから、![]() の分散が最も小さいことが分かります。
の分散が最も小さいことが分かります。








