2019年6月統計検定2級の問題の解説(その3)
2019/08/25
カテゴリ:統計検定
タグ:2019年6月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
問14 [25]
抽出したサンプルサイズをn、標本比率を![]() とすると、母比率pの95%信頼区間は次の式から求められます。
とすると、母比率pの95%信頼区間は次の式から求められます。
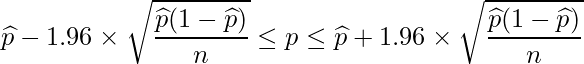
この式に、p=20/200=0.1、n=200の値を代入すると、比率の95%信頼区間は
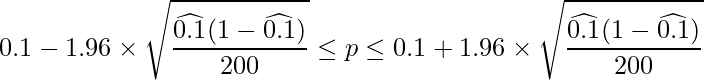
と計算できます。
問15 [26]
母分散が分からない場合、母集団の平均を![]() 、標本平均を
、標本平均を![]() 、不偏分散を
、不偏分散を![]() 、抽出したサンプルサイズをn、信頼係数を
、抽出したサンプルサイズをn、信頼係数を![]() とすると、次の式から母平均
とすると、次の式から母平均![]() の
の![]() 信頼区間を求めることができる。ただし、「
信頼区間を求めることができる。ただし、「![]() 」は「自由度が
」は「自由度が![]() 」のt分布における上側確率が
」のt分布における上側確率が![]() となる値(t値)を示す。
となる値(t値)を示す。
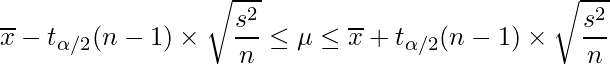
この式に、![]() =3.23、
=3.23、![]() 、n=24、α=0.05の値を代入すると、比率の95%信頼区間は
、n=24、α=0.05の値を代入すると、比率の95%信頼区間は
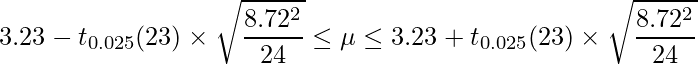
となります。「t分布のパーセント点」の自由度23の値から![]() を使って計算すると
を使って計算すると
となります。
問15 [27]
問題文より、片側t検定について考えます。
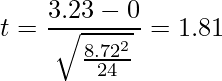
「t分布のパーセント点」の自由度23の値を見ると、![]() 、
、![]() であることから、有意水準5%では棄却できますが、2.5%では棄却できません。
であることから、有意水準5%では棄却できますが、2.5%では棄却できません。
問16 [28]
帰無仮説(θ=0)において![]() となる確率は、「標準正規分布の上側確率」より
となる確率は、「標準正規分布の上側確率」より![]() であることが分かります。すなわち、第1種過誤の確率は0.212です。
であることが分かります。すなわち、第1種過誤の確率は0.212です。
次に、対立仮説(θ=1)において![]() となる確率を求めます。
となる確率を求めます。
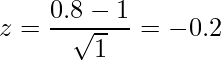
したがって、![]() であることが分かります。すなわち、第2種過誤の確率は0.421です。
であることが分かります。すなわち、第2種過誤の確率は0.421です。
問16 [29]
![]() のとき、
のとき、![]() 、
、![]()
![]() のとき、
のとき、![]() 、
、![]()
![]() のとき、
のとき、![]() 、
、![]()
また[28]より、![]() のとき、
のとき、![]() 、
、![]()
これらの情報より、![]() が増加すると
が増加すると![]() も増加すること、グラフの形は上に凸であることが分かります。
も増加すること、グラフの形は上に凸であることが分かります。
問16 [30]
[29]で求めた値を使うと、
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
![]() のとき、
のとき、![]()
となり、第1種過誤の確率と第2種過誤の確率の和を最小にする![]() は0.5であると考えられます。
は0.5であると考えられます。
問17 [31]
I:× 高校卒の学歴と初任給の関係は、C、U、Gの値をいずれも0とすることで計算することができます。
II:○ 回帰係数の値の差を求めます。7.180-4.450=2.73より2.73万円高い傾向があることが分かります。
III:× P値は自由度n-k-1のt分布を用いた検定結果です。このときnはサンプルサイズを、kは説明変数の数(切片は含まない)を表します。
問17 [32]
I:○ 正しいです。
II:× 自由度調整済み決定係数はn-k-1(nはサンプルサイズ、kは説明変数の数を表す)の値を使って決定係数の調整を行います。したがって、単回帰モデルにおいても決定係数と自由度調整済み決定係数は等しくなりません。
III:× 両側検定の場合と片側検定の場合では算出されるP値は異なります。
問17 [33]
I:× 説明変数の数が異なるモデル間で比較を行う場合には自由度調整済み決定係数を使います。
II:○ 正しいです。
III:○ 正しいです。
問18 [34]
Rの出力ではPr(>|t|)の部分が、偏回帰係数の有意性の検定の結果になります。すなわち、有意水準5%=0.05以下の変数が有意な変数になります。
問18 [35]
1:× Adjusted R-squaredは自由度修正済み決定係数を、Multiple R-squaredは決定係数を表します。正規性の検定の結果を表すものではありません。
2:× t valueはt分布における値です。t検定のために用いる値であって、変数の説明力を表すものではありません。
3:○ 解析結果を見ると、「car」の偏回帰係数は「-0.0077833」となっています。すなわち、1人あたりの乗用車数が多い場合には、1人あたりの小売店舗事業所数は少ない傾向にあることが分かります。
4:× F検定(回帰式の有意性の検定)における帰無仮説は、「回帰変動は0である(偏回帰係数はすべて0である)」です。定数項は含みません。
5:× 一般的にはAdjusted R-squared(自由度修正済み決定係数)を使います。







