2019年6月統計検定2級の問題の解説(その2)
2019/08/24
カテゴリ:統計検定
タグ:2019年6月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問8:確率(復元抽出)に関する問題
- 問9:確率変数の期待値と分散に関する問題
- 問10:幾何分布に関する問題
- 問11:正規分布を用いた確率計算に関する問題
- 問12:t分布を用いた確率計算に関する問題
- 問13:確率(復元抽出)と標本平均に関する問題
問8 [14]
袋Bから玉を取り出す確率は、「サイコロを1回投げて3以上の目が出た場合」なので4/6=2/3です。2回玉を取り出すので、1回目に赤玉、2回目に白玉が出る確率は、
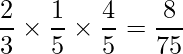
1回目に白玉、2回目に赤玉が出る確率は、
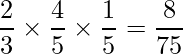
となることから、求める確率は足して16/75となります。
問8 [15]
まず、赤玉が2回取り出される確率を求めます。袋Aから玉を取り出す確率は、「サイコロを1回投げて2以下の目が出た場合」なので2/6=1/3です。また、袋Aから赤玉が取り出される確率は2/5です。したがって、袋Aから赤玉が2回取り出される確率は次のように計算できます。
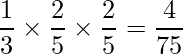
袋Bから玉を取り出す確率は、「サイコロを1回投げて3以上の目が出た場合」なので4/6=2/3です。また、袋Bから赤玉が取り出される確率は1/5です。したがって、袋Bから赤玉が2回取り出される確率は次のように計算できます。
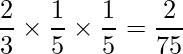
これらの確率を足した6/75が、赤玉が2回取り出される確率となります。
次に、赤玉が1回取り出される確率を求めます。袋Aが選ばれる場合、
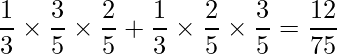
袋Bが選ばれる場合は[14]で求めたように16/75であることから、これらの確率を足した28/75が、赤玉が1回取り出される確率となります。したがって、赤玉が取り出される回数の期待値E(X)は次のように計算できます。
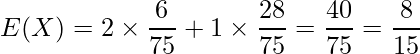
問9 [16]
XとYの共分散は次のように求められます。
Cov(X, Y)=E[XY]-E[X]E[Y]=4-1×2=2
2乗の期待値は、分散の式を使って求めます。
- V[Z]=V[X+Y]=V[X]+V[Y]+2Cov(X, Y)=24
- V[Z]=V[2X-Y]=4V[X]+V[Y]-4Cov(X, Y)=24
この式を解くと、V[X]=4、V[Y]=16となります。
であることを利用すると、![]() =5、
=5、![]() =20となります。
=20となります。
問9 [17]
XとYの相関係数は次ように求められます。
![Rendered by QuickLaTeX.com \displaystyle \rho= \frac{Cov(X,Y)}{\sqrt{V[X]V[Y]}} = \frac{2}{\sqrt{4 \times 16}} = \frac{2}{8} = 0.25](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-8ef31f622c29c5bac0d56748f77356e4_l3.png)
問10 [18]
調査対象者が在宅している確率が0.2なので、在宅していない確率は0.8になります。3軒目の訪問ではじめて調査対象者が在宅している確率は、0.8×0.8×0.2=0.13となります。
問10 [19]
初めて調査対象者が在宅しているまでに訪問する軒数の確率分布は「幾何分布」です。「幾何分布」とは、成功確率がpである独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数Xが従う確率分布のことです。
確率変数Xが成功確率pの幾何分布に従っている時、その期待値E(X)は次の式から求められます。
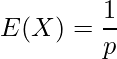
したがって、期待値はE(X)=1/0.2=5となります。
問11 [20]
期待値2、分散9の正規分布において、確率変数Xが![]() となる確率は、
となる確率は、
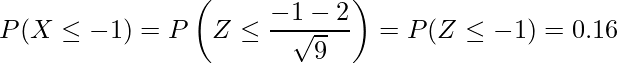
となります。Zは標準正規分布に従う確率変数であり、「標準正規分布の上側確率」を用いて値を得ます。
同様にして、確率変数Xが![]() となる確率は、
となる確率は、
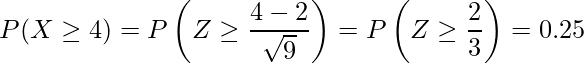
となります。したがって、![]() となる確率は、1-0.16-0.25=0.59となります。
となる確率は、1-0.16-0.25=0.59となります。
問12 [21]
問題文より、標本平均に注目していることからt分布を用いることを考えます。
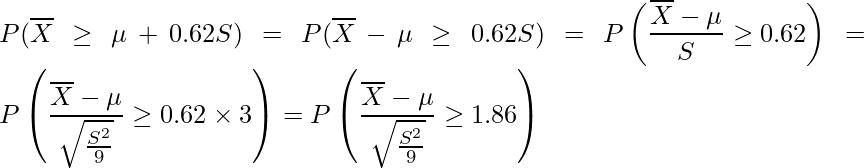
と変形できます。「t分布のパーセント点」より、自由度8のときに確率変数Xが1.86以上となる確率は0.05であることが分かります。
問13 [22]
![]() となるのは、
となるのは、![]() が6となる場合です。これは、
が6となる場合です。これは、![]() もしくは
もしくは![]() の2通りです。
の2通りです。
したがって、確率は
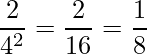
となります。同様に、![]() となるのは、
となるのは、![]() が12となる場合です。これは、
が12となる場合です。これは、![]() 、
、![]() 、
、![]() の3通りです。
の3通りです。
したがって、確率は
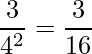
となります。
問13 [23]
中心極限定理より、![]() の平均(期待値)=中央値=最頻値と考えることができます。
の平均(期待値)=中央値=最頻値と考えることができます。![]() の最小値は
の最小値は![]() のときで2、最大値は
のときで2、最大値は![]() のときで8です。
のときで8です。
したがって、![]() の平均(期待値)=中央値=最頻値=(2+8)/2=5となります。
の平均(期待値)=中央値=最頻値=(2+8)/2=5となります。
問13 [24]
[23]より、![]() の期待値は5と計算できます。
の期待値は5と計算できます。
このとき、![]() をすべて計算する必要はありません。また、
をすべて計算する必要はありません。また、![]() を抽出したデータも不要です。
を抽出したデータも不要です。








