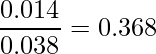※統計検定2級 解説記事一覧はこちら※

下記のリンクからそれぞれの問題の解説に飛ぶことができます。

• 問1：相対度数分布表に関する問題
• 問2：折れ線グラフと相関係数に関する問題
• 問3：価格指数と移動平均に関する問題
• 問4：ラスパイレス価格指数に関する問題
• 問5：標本抽出に関する問題
• 問6：標本抽出法に関する問題
• 問7：条件付き確率に関する問題

問1 [1]

相対度数分布表なので、各項目の割合(%)をすべて足すと100%になります。したがって、

• （ア）=100-(85.1+2.1)=12.8(%)
• （イ）=100-(76.6+17.0+2.1)=4.3(%)

となります。

問1 [2]

箱ひげ図に関する問題です。最大値に着目するとすんなりと解けます。

• Aのグラフ：最大値は約70→最大値が「60校以上80校未満」である1952年
• Bのグラフ：最大値は約100→最大値が「100校以上120校未満」である1985年
• Cのグラフ：最大値は約140→最大値が「120校以上140校未満」である2017年

問1 [3]

Ⅰ：×
四分位範囲は箱ひげ図の箱の高さで示されています。1952年よりも1985年の方が、1985年よりも2017年の方が、四分位範囲は大きいです。

Ⅱ：×
1952年の都道府県別の大学数の最大値は約70で、1985年の都道府県別の大学数の最大値は約100です。

Ⅲ：○
中央値は箱ひげ図の箱の中の太線で示されています。1952年よりも1985年の方が、1985年よりも2017年の方が、中央値は大きいです。

問2 [4]

折れ線グラフから相関関係を読み取る問題です。

Ⅰ：〇
グラフを見ると、「男性・正社員」のグラフは放物線を描いていることが分かります。このような場合には、相関係数だけから相関の強さを判断してはいけません。

Ⅱ：×
「女性・正社員」の20歳～54歳のデータは、20～69歳のデータと比べて直線的な関係がより強い（単純増加している）ことが分かります。したがって、相関係数は0.56よりも大きくなることが予想されます。

Ⅲ：×
相関係数は2つの変数間の直線的な関係の強さを示すものであり、が1増加したときにがどの程度増加するかを示すものではありません。

問3 [5]

2016年12月に対する2017年1月の変化率が4.98%であることを使います。2016年12月の不動産価格指数をとおくと、

となります。この式を解くと次のようになります。

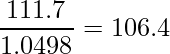
問3 [6]

3項移動平均は中心となる項と前後の項を1つづつ、計3つの項を足したものを3で割ることで算出できます。移動平均の詳細についてはこちらをご覧ください。

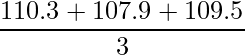
問4 [7]

ラスパイレス価格指数は次の式から算出できます。

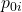• ：基準年の価格　　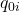：基準年の数量
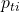• ：比較年の価格　　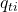：比較年の数量

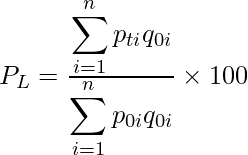
したがって、正しい計算式は次のようになります。

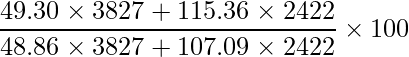
ラスパイレス価格指数を含む様々な指数の詳細についてはこちらをご覧ください。

問5 [8]

標本抽出に関する基礎的な知識を問う問題です。

Ⅰ：〇
正しいです。

Ⅱ：×
例えばAの層には10人、Bの層には1000人が含まれる場合、それぞれの層の人数を無視して標本抽出を行う（A層から5人、B層から5人抽出する等）と、標本は偏ったものになってしまいます。

Ⅲ：〇
例えば男性が非常に少ない集団から単純無作為抽出によって標本を得る場合、標本の中に男性が含まれない可能性があります。

問6 [9]

母集団をいくつかのグループに分け、そこから無作為抽出でいくつかグループを選び、さらにその中から無作為抽出でいくつかのグループを選び・・・という操作を繰り返して、最終的に選ばれたグループの中から調査対象を無作為抽出する方法を「多段抽出」といいます。

無作為抽出過程が二段階である場合、この方法を「二段抽出」といいます。

問7 [10]

工場Aで生産したクッキーのはこの中にカモノハシの絵がプリントされている確率は次のように計算できます。

同様に、工場Bで生産したクッキーのはこの中にカモノハシの絵がプリントされている確率は次のように計算できます。

したがって、クッキーの箱を無作為に1個抽出したときに、カモノハシの絵がプリントされているクッキーが入っている確率は次のようになります。

問7 [11]

求める確率は、「カモノハシの絵がプリントされているクッキーが入っている確率」における「そのクッキーが工場Aで生産された確率」です。