2018年11月統計検定2級の問題の解説(その2)
2019/01/01
カテゴリ:統計検定
タグ:2018年11月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
問8 [12]
問8はやや難問でした。
Uは平均0、分散1の正規分布に従うことから、![]() (Uが-1.64以上となる確率は0.95)となります。したがって、
(Uが-1.64以上となる確率は0.95)となります。したがって、
問8 [13]
「Uは平均0、分散1の正規分布に従う」という条件を使って解いていきます。問題文より、
Uにおける上側5%点は次のように表すことができます。
したがって、
となります。xとYとの関係は一次関数なので、この関係を適切に表しているのは①であることが分かります。
問9 [14]
問9は計算がとてもめんどくさい問題です。計算ミスをしないようにしましょう。
サイコロを1回投げたときに、2以下の目が出る確率は1/3、3以上の目が出る確率は2/3です。したがって、
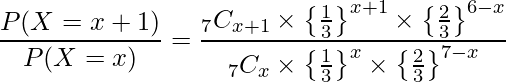
この式を展開すると、次のようになります。
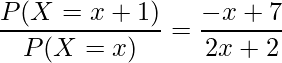
問9 [15]
[14]で計算した比を使います。
- x=0のとき:7/2 → P(X=0) < P(X=1)
- x=1のとき:6/4 → P(X=1) < P(X=2)
- x=2のとき:5/6 → P(X=2) > P(X=3)
- x=3のとき:4/8 → P(X=3) > P(X=4)
- x=4のとき:3/10 → P(X=4) > P(X=5)
- x=5のとき:2/12 → P(X=5) > P(X=6)
- x=6のとき:1/14 → P(X=6) > P(X=7)
この結果より、x=2のときにP(X=x)は最大となることが分かります。
問10 [16]
標本平均![]() の期待値は次のように計算できます。
の期待値は次のように計算できます。
![Rendered by QuickLaTeX.com \displaystyle E[\overline{X}] = E \left[\frac{X_1 + X_2 + \cdots + X_n}{n}\right] = \frac{E[X_1] + E[X_2] + \cdots + E[X_n]}{n}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-2563eac41c062a0a433fc673dad9e7df_l3.png)
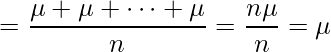
標本平均![]() の分散は次のように計算できます。
の分散は次のように計算できます。
![Rendered by QuickLaTeX.com \displaystyle V[\overline{X}] = V \left[\frac{X_1 + X_2 + \cdots + X_n}{n}\right] = \frac{V[X_1] + V[X_2] + \cdots + V[X_n]}{n^2}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7d48abc4ba0e1557ec76a3fee00c99a3_l3.png)
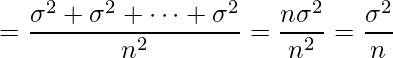
問11 [17]
難問でした。歪度と尖度の問題はおそらく統計検定2級では久しぶりに(初めて?)出たような気がします。出題範囲には入っていますが、ここまできっちり勉強していた受験生は少ないのではないでしょうか。
【歪度】分布が正規分布からどれだけ歪んでいるかを表す統計量で、左右対称性を示す指標のことです。「右裾が長い」もしくは「左に偏った」分布のときには正の値を、「左裾が長い」もしくは「右に偏った」分布のときには負の値をとります。左右対称の分布(例えば正規分布)の場合には0になります。
【尖度】分布が正規分布からどれだけ尖っているかを表す統計量で、山の尖り度と裾の広がり度を示します。正規分布より尖った分布(データが平均付近に集中し、分布の裾が重い)のときには正の値を、正規分布より扁平な分布(データが平均付近から散らばり、分布の裾が軽い)のときには負の値をとります。正規分布の場合には0になります。
問11 [18]
確率変数Xが一様分布U(-1, 1)に従うとき、確率密度関数は
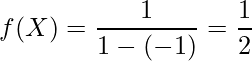
となります。期待値と分散は定義より
![Rendered by QuickLaTeX.com \displaystyle \mu = E[X] = \frac{1+(-1)}{2} = 0](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-60994ec9d805aada4936eb066004e0f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \sigma^2 = V[X] = \frac{(-1-1)^2}{12} = \frac{1}{3}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-2b529b5d8edc0d089d8249597d1c54b9_l3.png)
問題文の定義を用いて歪度を求めると
![Rendered by QuickLaTeX.com \displaystyle \frac{E[(X-\mu)^3]}{\sigma^3} = \frac{E[(X-0)^3]}{\sigma^3} = \frac{E[X^3]}{\sigma^3} = \frac{\int_{-1}^1 x^3f(x)dx}{\sigma^3} = \frac{0}{\sigma^3} = 0](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-e04c2b385656cc0b99ed54416b1e3fbe_l3.png)
となります。また、問題文の定義を用いて尖度を求めると
![Rendered by QuickLaTeX.com \displaystyle \frac{E[(X-\mu)^4]}{\sigma^4}-3 = \frac{E[(X-0)^4]}{\left\{\frac{1}{3}\right\}^2}-3 = \frac{E[X^4]}{\frac{1}{9}}-3](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-54ac3aa6e0cd369bf78c6615ff66a803_l3.png)
![Rendered by QuickLaTeX.com \displaystyle = 9 \times \int_{-1}^1 x^4f(x)dx}-3 = 9 \times \left[\frac{1}{5}x^5\times \frac{1}{2} \right]^1_{-1} -3 = \frac{9}{5} -3 = -1.2](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-4cb7e65c3c3c3fb2125dfadbfe0a6986_l3.png)
となります。
問11 [19]
Ⅰ:× 右に裾が長い分布では歪度は正の値に、左に裾が長い分布では歪度は負の値になります。
Ⅱ:× 正規分布よりも尖っている分布では尖度は正の値に、正規分布よりも中心部が平坦な分布では尖度は負の値になります。
Ⅲ:× 自由度が大きくなるにつれて、t分布は正規分布に近づきます。すなわち、尖度は0に近づきます。
問12 [20]
比率の信頼区間を求める問題はよく出題されます。詳しい説明はこちらをご覧ください。
サンプルサイズn=1,338、標本比率![]() =0.02であることから、求める信頼区間は次のようになります。
=0.02であることから、求める信頼区間は次のようになります。
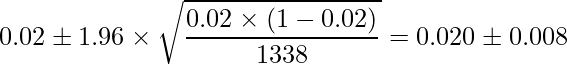
問13 [21]
サンプルサイズをn、母平均を![]() 、標本平均を
、標本平均を![]() 、不偏分散を
、不偏分散を![]() とすると、t統計量は次の式から求められます。
とすると、t統計量は次の式から求められます。
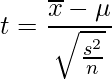
このとき使用するのは自由度「n-1」のt分布です。母平均の検定の詳しい説明はこちらをご覧ください。
問題文より、
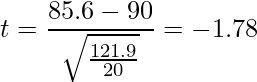
自由度19のt分布の上側2.5%点は2.093なので、|t|<2.093となることから、帰無仮説は棄却されません。








