2018年11月統計検定2級の問題の解説(その3)
2019/01/04
カテゴリ:統計検定
タグ:2018年11月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
問14 [22]
等分散性の検定では、2つの群の不偏分散をそれぞれ![]() 、
、![]() 、サンプルサイズを
、サンプルサイズを![]() 、
、![]() とすると、F統計量は次の式から計算できます。
とすると、F統計量は次の式から計算できます。
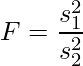
このとき使用するのは自由度「![]() 」のF分布です。
」のF分布です。
問14 [23]
【第一種の過誤】統計的仮説検定において、帰無仮説が真であるのにもかかわらず帰無仮説を偽として棄却してしまう誤りのことです。
有意水準を5%とした場合、3つの検定のうちいずれか1つの検定で帰無仮説が棄却されてしまう確率は次のように計算できます。
問15 [24]
二項分布において、確率変数Xの期待値と分散は次の式から求められます。問題文より、サンプルサイズn=200、不良品率p=0.05です。
問15 [25]
標本比率を![]() 、母比率を
、母比率を![]() 、サンプルサイズをnとすると、次の式から求められるz統計量は標準正規分布に従います。
、サンプルサイズをnとすると、次の式から求められるz統計量は標準正規分布に従います。
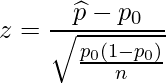
問題文より、標本比率は16/200=0.08、母比率は0.05、サンプルサイズは200です。したがって、
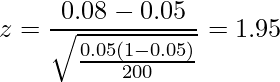
標準正規分布表を見ると、標準正規分布に従うuが取る値が1.95以上となる確率は![]() であることが分かります。
であることが分かります。
問15 [26]
2つの群の標本比率をそれぞれ![]() 、
、![]() 、サンプルサイズを
、サンプルサイズを![]() 、
、![]() とすると、次の式から求められるz統計量は標準正規分布に従います。
とすると、次の式から求められるz統計量は標準正規分布に従います。
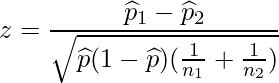
ただし、![]() はプールした標本比率を表します。
はプールした標本比率を表します。
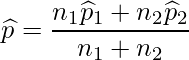
問題文より、A社の標本比率は0.08、B社の標本比率は17/200=0.085、サンプルサイズはいずれも200です。したがって、プールした標本比率![]() は
は
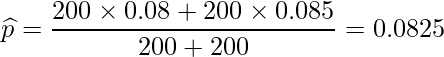
となります。これを用いてz統計量を算出すると、
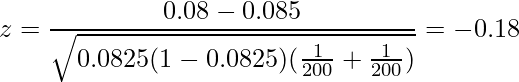
となります。標準正規分布表を見ると、標準正規分布に従うuが取る値が0.18以上となる確率(-0.18以下となる確率と同じです)は![]() であることが分かります。この問題では両側検定を行うことを想定しているので、P値は0.43×2=0.86と計算できます。
であることが分かります。この問題では両側検定を行うことを想定しているので、P値は0.43×2=0.86と計算できます。
問16 [27]
適合度検定において、カイ二乗統計量は「「理論値」からの「実測値」のズレを2乗したものを、「理論値」の値で割ったものの総和」として算出します。適合度検定の詳しい説明はこちらをご覧ください。
問16 [28]
適合度検定では、カイ二乗統計量が自由度「カテゴリーの数-1」のカイ二乗分布に従うことを使います。
この問題ではカテゴリーの数が6個なので、自由度6-1=5のカイ二乗分布を使って片側検定を行います。カイ二乗分布表より、自由度5のカイ二乗分布における上側5%点は11.07です。[27]の計算結果より![]() であることから、有意水準5%において帰無仮説は棄却されないという結果になります。
であることから、有意水準5%において帰無仮説は棄却されないという結果になります。
問17 [29]
Rによる出力に慣れていないと難しい問題でした。
この問題で見るべきポイントは「Residual standard error」です。これは残差の標準誤差(103.5)と自由度(52)を示したものです。この自由度は「サンプルの数-説明変数の数-1」から算出できます。
この問題では、分析に用いた国の数-2(説明変数の数)-1=52より、分析に用いた国の数は55と計算できます。
問17 [30]
Ⅰ:× αの推定値の標準誤差は1.137e+02=113.7です。
Ⅱ:〇 3つのパラメータはすべてP値(Pr(>|t|))が0.05より小さくなっています。
Ⅲ:× 自由度調整済み決定係数の値は「Adjusted R-squared」に記載されています。「Multiple R-squared」に記載されているのは決定係数です。
問17 [31]
Ⅰ:〇 「population」の偏回帰係数(Estimate)の値が負になっているので正しいです。
Ⅱ:〇 「log(gdp)」の偏回帰係数の値が正になっているので正しいです。
Ⅲ:〇 出力結果より、重回帰モデルは「自動車普及率=-1283-0.06×人口密度+175.7×log(1人当たりのGDP)」であることが分かります。この式に人口密度=400とlog(1人当たりのGDP)=10を代入すると、自動車普及率=-1283-0.06×400+175.7×10=450となります。
問18 [32]
かなり難しい問題でした。重回帰分析をきちんと理解しておかないと解けない問題です。
Ⅰ:〇
残差の標準誤差![]() =残差平方和/(サンプルの数-説明変数の数-1)という計算式を用いて、残差平方和を計算します。すなわち、残差平方和=
=残差平方和/(サンプルの数-説明変数の数-1)という計算式を用いて、残差平方和を計算します。すなわち、残差平方和=![]() となります。
となります。
Ⅱ:× すべての値を1万倍してもt値は変化しません。
Ⅲ:〇 すべての値を1万倍した場合、偏回帰係数の値も1万倍になります。
問18 [33]
Ⅰ:× 説明変数が不要かどうかは、一般的にP値を見て判断します。
Ⅱ:× 説明変数間の相関係数が非常に高い場合、多重共線性が発生している可能性が高いです。
Ⅲ:× P値が5%よりも大きいので、帰無仮説は棄却されません。
問18 [34]
Ⅰ:× 異なる回帰モデルを用いた場合、同じ変数の偏回帰係数は必ずしも同じ値になりません。
Ⅱ:〇 見かけ上の相関が疑われる場合、誤った結論を導いてしまう可能性があるので注意が必要です。
Ⅲ:× 有意ではない場合、「zが一定の場合、xが1万円大きいときyが6.462万円小さくなる」とは言えません。







