2019年6月統計検定2級の問題の解説（その1）

2019/06/29

カテゴリ：統計検定

※統計検定2級解説記事一覧はこちら※

下記のリンクからそれぞれの問題の解説に飛ぶことができます。

問1：相対度数分布表に関する問題
問2：相関係数と共分散に関する問題
問3：データ変換に関する問題
問4：相関係数と偏相関係数に関する問題
問5：フィッシャーの3原則に関する問題
問6：標本抽出法に関する問題
問7：様々な事象に関する問題

問1 [1]

2008年における貯蓄額が2000万円以上の世帯は19.6%なので、

（イ）=19.6-(5.3+3.8+4.7)=5.8(%)

となります。

問1 [2]

2015年の相対度数のデータから、中央値、すなわち累積相対度数が50%となる階級を探します。

（A）から（G）までの累積相対度数=13.2+7.2+7.0+6.1+5.6+5.5+4.5=49.1(%)
（A）から（H）までの累積相対度数=13.2+7.2+7.0+6.1+5.6+5.5+4.5+4.2=53.3(%)

となることから、中央値が含まれる階級は「700万円以上800万円未満」の階級となります。

問1 [3]

2015年における「100万円未満」から「1000万円以上1200万円未満」までの相対度数を足すと、

13.2+7.2+7.0+6.1+5.6+5.5+4.5+4.2+3.3+3.2+6.0=65.8(%)

です。「1200万円以上1400万円未満」の階級の4.6%はこの階級の中で一様分布していると仮定します。すなわち、「1200万円以上1300万円未満」の割合は2.3%程度であると予想されます。したがって、求める値は

13.2+7.2+7.0+6.1+5.6+5.5+4.5+4.2+3.3+3.2+6.0+2.3=68.1≒70(%)

となります。

問2 [4]

国語と数学の得点の相関係数は0.72であることから、強い正の相関があることが分かります。①～⑤の中で正の相関が見られるのは③④⑤です。この中で、⑤は非常に強い相関が、③は弱い相関がある場合の散布図です。相関係数の詳細についてはこちらをご覧ください。

問2 [5]

2つの要素xとyからなるn個のデータ（ $x_{i}$ , $y_{i}$ : i=1, 2,…, n）が得られたとき、その相関係数 $r_{xy}$ は次の式から算出されます。

$r_{xy}=\frac{\displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\displaystyle \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\overline{x})^{2}} \times \sqrt{\displaystyle\frac{1}{n} \sum_{i=1}^{n} (y_{i}-\overline{y})^{2}}}$

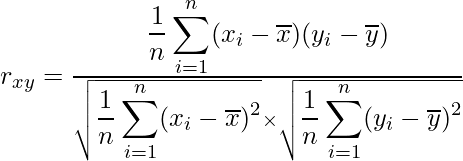
この式の分子はxとyの「共分散」です。分母はx、yそれぞれの標準偏差の積になっています。したがって共分散 $s_{xy}$ は、

$\displaystyle 0.72= \frac{s_{xy}}{12.5 \times 16.4}$

を解いて、 $s_{xy}$ =147.6となります。

問2 [6]

数学の点数yを2倍したものをY=2yとおきます。Yの標準偏差 $\rho_{Y}$ は

$\begin{eqnarray*} \rho_{Y} &=& \sqrt{\displaystyle \frac{1}{n} \sum_{i=1}^{n}{(Y_{i}- \overline{Y})^{2}}} = \sqrt{\displaystyle \frac{1}{n} \sum_{i=1}^{n}{(2y_{i}- \overline{2y})^{2}}} \\ &=&　\sqrt{\displaystyle \frac{1}{n} \sum_{i=1}^{n}{4(y_{i}- \overline{y})^{2}}} = 2 \time \sqrt{\displaystyle \frac{1}{n} \sum_{i=1}^{n}{(y_{i}- \overline{y})^{2}}} = 2\rho_{y} \end{eqnarray*}$

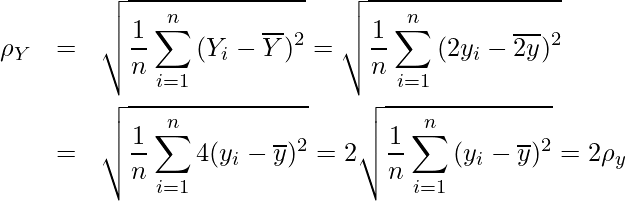
となります。Yの平均も当然2倍になりますので、変動係数 $CV_{Y}$ は

$CV_{Y}=\displaystyle \frac{\rho_{Y}}{\bar{Y}} = \frac{2\rho_{y}}{2\bar{y}} = \frac{\rho_{y}}{\bar{y}}$

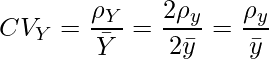
となります。同様に考えると、国語の点数xと数学の点数を2倍にしたものYとの共分散 $s_{xY}$ は、

$\begin{eqnarray*} s_xY &=& \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\overline{x})(Y_{i}-\overline{Y}) \\ &=& \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\overline{x})(2y_{i}-2\overline{y}) \\ &=& 2 \times \frac{1}{n} \sum_{i=1}^{n} (x_{i}-\overline{x})(y_{i}-\overline{y}) = 2s_{xy} \end{eqnarray*}$

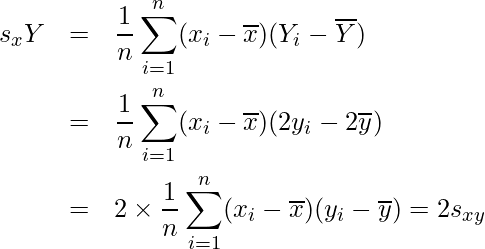
問3 [7]

Ⅰ：○
標準化得点は、平均が0、分散が1となるように元のデータを変換したものです。

Ⅱ：×
例えば、マイアミの摂氏22を標準化すると(22-2.4)/7.0=2.8になります。

Ⅲ：○

$\begin{eqnarray*} w_i &=& \frac{F_i-(1.8 \times 2.4 + 32)}{1.8 \times 7.0} \\ &=& \frac{(1.8C_i + 32)-(1.8 \times 2.4 + 32)}{1.8 \times 7.0} \\ &=& \frac{1.8C_i - 1.8 \times 2.4}{1.8 \times 7.0} \\ &=& \frac{C_i - 2.4}{7.0} = z_i \\ \end{eqnarray*}$

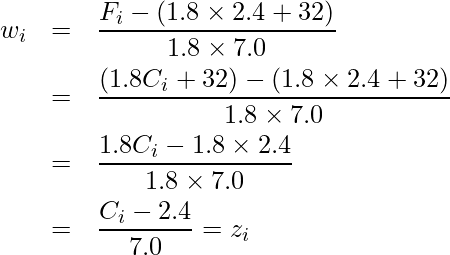
問3 [8]

華氏（F）は摂氏（C）を1.8倍して32を足したものなので、平均値 $\overline{F}$ も $\overline{C}$ に1.8倍して32を足したものになります。

一方、元のデータに定数を足しても標準偏差は変化しませんが、元のデータを定数倍すると標準偏差は定数倍になります。したがって、 $s_F$ は $s_C$ を1.8倍したものになります。

問4 [9]

Ⅰ：○

Ⅱ：×
偏相関係数は、見かけ上の相関がある場合に第3の因子の影響を除いた相関係数のことです。非線形関係を捉えるものではありません。

Ⅲ：×
相関係数と偏相関係数の符号は一致する場合も一致しない場合もあります。問題文の結果では、相関係数も偏相関係数も正であったことから、世帯人員と持家率との間には正の相関があることが分かります。

問4 [10]

Ⅰ：×
誤りです。

Ⅱ：×
誤りです。

Ⅲ：○
偏相関係数に関する正しい解釈です。偏回帰係数の詳細についてはこちらをご覧ください。

問5 [11]

Ⅰ：○
正しいです。「無作為化」とは、実験の順序や場所などが複数ある場合に、比較したい処理群を無作為に（ランダムに）割り付けることです。目的とする要因以外に結果に影響を与える要因がある場合に、無作為化によってその影響の偏りをできるだけ小さくすることができます。

Ⅱ：×
誤りです。「繰り返し」とは、複数の処理を比較する際に、それぞれの処理に対して同じ条件で2回以上の繰り返し実験（評価）を行うことです。同一実験条件に複数の被験者を割り当てても問題ありません。

Ⅲ：×
誤りです。「局所管理」とは、実験を行う時間や場所を区切ってブロックを作り、そのブロック内でのバックグラウンドができるだけ均一になるように管理することです。フィッシャーの3原則の詳細についてはこちらをご覧ください。

問6 [12]

1：×
「多段抽出」では、段数を増やすほど標本に偏りが生じる可能性が高くなります。

2：×
「系統抽出」とは、通し番号をつけた名簿を作成し、1番目の調査対象を無作為に選び、2番目以降の調査対象を一定の間隔で抽出する方法のことです。

3：×
回答率が低い場合、得られたデータに偏りが生じる可能性が高くなります。

4：×
系統抽出では、名簿の並び順に何らかの周期があると標本に偏りが生じる可能性があります。したがって、単純無作為抽出した標本による調査結果のほうが精度が高いといえます。

5：○
正しいです。標本の抽出方法の詳細についてはこちらをご覧ください。

問7 [13]

P(A)=0.4、P(B)=0.35、P(A∪B)=0.61であることから、P(A)+P(B)-P(A∩B)=P(A∪B)を解いて、P(A∩B)=0.14となります。すなわち、P(A)×P(B)=P(A∩B)が成り立つので、事象Aと事象Bは独立であるといえます。

一方、排反事象とは「同時に起こらない」事象のことです。P(A∩B)≠0であることから、事象Aと事象Bは排反ではありません。

ブログ