2019年11月統計検定2級の問題の解説(その3)
2019/11/30
カテゴリ:統計検定
タグ:2019年11月
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問13:比率の信頼区間に関する問題
- 問14:相対度数分布表に関する問題
- 問15:比率の信頼区間とサンプルサイズに関する問題
- 問16:片側t検定に関する問題
- 問17:一元配置分散分析に関する問題
- 問18:重回帰モデルに関する問題
問13 [22]
母比率の信頼区間は次の式から求められます。ただし、![]() を標本比率、nをサンプルサイズとします。
を標本比率、nをサンプルサイズとします。
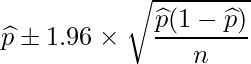
問題文より標本比率は0.54、サンプルサイズは100であることから、
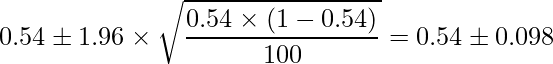
と計算できます。
問14 [23]
相対度数を「300万円以上400万円未満」の階級まで足すと46.5%になります。また、「400万円以上500万円未満」の階級まで足すと56.9%になります。したがって、中央値は「400万円以上500万円未満」の中に含まれると考えられます。
中央値の半分に満たない所得は「100万円未満」「100万円以上200万円未満」と、「200万円以上300万円未満」の一部であると考えられます。したがって、中央値の半分に満たない所得の世帯割合は6.2+13.4=19.6%から19.6+13.7=33.3%の間であると考えられます。
問14 [24]
中心極限定理より、母集団が正規分布に従わない場合でも、標本が十分に大きい場合には標本平均の分布は正規分布に従います。したがって、nが十分に大きい場合には、母平均![]() の信頼区間は標準正規分布のパーセント点を用いて作成することができます。
の信頼区間は標準正規分布のパーセント点を用いて作成することができます。
問15 [25]
母比率の信頼区間の幅は次の式から算出できます。詳しくは「21-4. 必要なサンプルサイズ」をご覧ください。
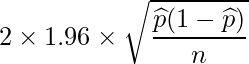
問題文より、政党の支持率について事前の情報がまったくないため、母比率の信頼区間の幅が最も大きくなる![]() を使います。
を使います。
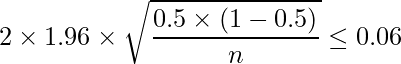
この式を解いて
となります。
問15 [26]
問題文より、政党の支持率がおよそ80%であることが分かっていることから、![]() を使います。
を使います。
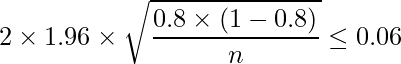
この式を解いて
となります。
問16 [27]
母平均![]() 、母分散
、母分散![]() の正規分布を母集団分布とする母集団から大きさ16の無作為標本を抽出していることから、統計量Tは「自由度16-1=15」の「t分布」に従います。
の正規分布を母集団分布とする母集団から大きさ16の無作為標本を抽出していることから、統計量Tは「自由度16-1=15」の「t分布」に従います。
問16 [28]
体重が減少するかどうかだけを検証する(体重が増加するかどうかについては検証しない)ので、片側検定を行います。帰無仮説は「食品Aの摂取後の体重に変化はない(![]() )」とします。帰無仮説が棄却されたときに採択される対立仮説は「食品Aの摂取後に体重が減少する(
)」とします。帰無仮説が棄却されたときに採択される対立仮説は「食品Aの摂取後に体重が減少する(![]() )」となります。
)」となります。
統計学では、背理法(最初に仮説を設定し、仮説が正しいとした条件で考えて矛盾が起こった場合に仮説が間違っていると判断する方法)を用いて検定を行います。
問16 [29]
問題文より、統計量tを求めます。
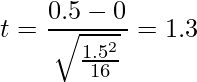
「t分布のパーセント点」の自由度15の値を見ると、![]() であることから、有意水準5%では帰無仮説を棄却できません。すなわち、対立仮説を採択することはできません。
であることから、有意水準5%では帰無仮説を棄却できません。すなわち、対立仮説を採択することはできません。
※検定により帰無仮説が棄却できない場合、これは帰無仮説が正しいと結論づけてよいということを意味しません。検定で用いられる方法は「背理法」なので、「帰無仮説が棄却されない」ことは「帰無仮説が正しいと結論づけてよい」ということにはならないのです。この場合、「対立仮説が正しいと結論づけることはできない」ということしか言えません。
問17 [30]
分散分析のポイントは「データ全体の平均値から各水準の平均値がどのくらいずれているか」を見ることです。そのため、「データ全体の平均値からの各データのズレ」を①「データ全体の平均値からの各水準の平均値のズレ(水準間平方和)」と②「それ以外のズレ(各水準の平均値からの各データのズレ)(残差平方和)」の2つに分け、①が②に対して大きいかどうかを検定によって検証します。
問17 [31]
「水準間」の自由度は、水準の個数から1を引いたものです。したがって「12-1=11」になります。
「残差」の自由度は「全体」の自由度から「水準間」の自由度を引いたものです。「全体」の自由度は、全てのデータの個数から1を引いたものなので「132-1=131」になります。したがって、「残差」の自由度は「131-11=120」になります。
問17 [32]
一元配置分散分析における帰無仮説は「すべての水準の母平均が等しい」であり、対立仮説は「少なくとも1つの水準の母平均が異なる(全ての水準のうち母平均が異なる水準がある)」です。「全ての水準の母平均は互いに異なる」ではないことに注意が必要です。
問題文よりF-値は3.0471であり、![]() および
および![]() よりも大きいことから、有意水準5%、2.5%いずれにおいても有意であり、帰無仮説は棄却できます。
よりも大きいことから、有意水準5%、2.5%いずれにおいても有意であり、帰無仮説は棄却できます。
問18 [33]
「income」の偏回帰係数(Estimate)0.39は、「賞与を一定としたときに、定期収入が1万円増えると消費支出が約0.39万円増える傾向がある」ことを意味しています。偏回帰係数は、ある変数以外の値を一定としたときに、ある変数が1増加したときに予想される増減を表しています。
問18 [34]
I:○ 元のデータを回帰式に代入して得られた予測値と、元のデータとの差は「残差」とよばれます。残差の性質上、残差の総和は0なので、予測値の平均と元のデータの平均は等しくなります。
II:○ 問題文より、消費支出の平均は31.3であることから、「31.3=14.3931+0.4121×世帯主収入合計の平均」 となり、これを解いて世帯主収入合計の平均=41.0となります。
III:○ 「残差」は元のデータを回帰式に代入して得られた予測値と、元のデータとの差です。したがって、各予測値に各残差を加えると、元のデータと等しくなります。
問18 [35]
I:○ 2つの変数の偏回帰係数を等しくすると、1つの偏回帰係数で回帰式を表すことができるため、これは単回帰モデルに他なりません。
II:× 自由度調整済み決定係数は「Adjusted R-squared」で表される値です。この値は重回帰モデルでは0.5161、単回帰モデルでは0.5261であることから、単回帰モデルのほうが大きいです。
III:○ 正しいです。








