2019年11月統計検定2級の問題の解説（その1）

2019/11/30

カテゴリ：統計検定

タグ：2019年11月

※統計検定2級解説記事一覧はこちら※

下記のリンクからそれぞれの問題の解説に飛ぶことができます。

問1：箱ひげ図に関する問題
問2：散布図とヒストグラムに関する問題
問3：指数を用いた変化率の計算に関する問題
問4：時系列データの変動に関する問題
問5：コレログラムに関する問題
問6：標本の抽出方法に関する問題

問1 [1]

箱ひげ図から東京の平均気温について分かることは、

外れ値の○の位置から、最大値は18℃未満である
外れ値の○の数から、16℃以上18℃未満の度数は「2」である

という2点です。この条件に合うのは(A)のみです。

問1 [2]

1：×
「範囲」とは、最大値と最小値の差のことです。この範囲が最も大きい都市は福岡であり、広島は最も小さい都市です。

2：×
「四分位範囲」とは、75パーセンタイル（第三四分位数）と25パーセンタイル（第一四分位数）の差のことです。すなわち、箱ひげ図の箱の高さに該当します。この四分位範囲が最も小さい都市は東京です。

3：○
「第一四分位数」は箱ひげ図の箱の底辺に該当します。底辺の位置が最も高い都市は福岡です。

4：×
「中央値」は箱ひげ図の箱の中の太線に該当します。太線の位置が最も低い都市は名古屋です。

5：×
「最大値」は箱ひげ図のひげの上端、もしくは外れ値がある場合には最も高い位置にある値に該当します。最大値が最も小さい都市は名古屋です。

問2 [3]

1：×
1990年において、女性の50歳時未婚率が8%を超えている都道府県は1つのみです。男性の場合、50歳時未婚率が8%を超えている都道府県は2つあります。

2：×
1990年において、男性の50歳時未婚率が10%を超えている都道府県は2つあります。

3：×
散布図において、どの点がどの都道府県を指しているかは分かりません。したがって、ある都道府県における2015年の値と1990年の値を比較することはできません。

4：○
2015年において、男性の50歳時未婚率の最小値は約18%です。同年の女性の50歳時未婚率の最大値は約19%であり、この都道府県を除くすべての都道府県において「女性の50歳時未婚率＜男性の50歳時未婚率」となります。ただし、女性の50歳時未婚率が最大の約19%である都道府県は、男性の50歳時未婚率が約26%であることから、この都道府県も含めて、「女性の50歳時未婚率＜男性の50歳時未婚率」であるといえます。

5：×
2015年において、女性の50歳時未婚率が最も低い都道府県は、男性の50歳時未婚率が3番目に低いです。

問2 [4]

1990年も、2015年もともに正の相関が見られますが、はっきりとした直線関係が見られるわけではないことから、弱い相関があると考えられます。弱い相関がある場合、相関係数は0.4前後になります（強い相関がある場合には0.8前後になります）。

ここで注意しなくてはならないのが、1990年には右上に外れ値があるという点です。この点は、直線関係をより明確にしていると考えられます。すなわち、この外れ値の影響により、相関係数が大きくなってしまっていると考えられます。

相関係数は、外れ値の影響を受けやすいため注意が必要です。詳しくは「外れ値と相関係数」をご覧ください。

問2 [5]

2015年における女性の50歳時未婚率の散布図から分かることは、

最大値は約19%である
18%～20%の度数は「1」である
8%～10%の度数は「2～3」である
10%～12%の度数は「11～14」である

という点です。この条件に合うのは③です。

問3 [6]

平成31年1月の賃金指数の30年1月からの変化率は-0.97%であることから、平成31年1月の賃金指数は次のように計算できます。

$\displaystyle 102.6 \times (1-0.0097)$

平成31年1月の賃金指数の平成30年12月からの変化率をrとすると、

$\displaystyle 104.1 \times \frac{100+r}{100} = 102.6 \times (1-0.0097)$

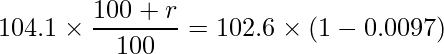
となります。この式を整理すると、

$\displaystyle 104.1 \times (100+r) = 100 \times \left\{ 102.6 \times (1-0.0097) \right\}$

$\displaystyle 100+r = 100 \times \left\{ \frac{102.6 \times (1-0.0097)}{104.1} \right\}$

$\displaystyle r = 100 \times \left\{ \frac{102.6 \times (1-0.0097)}{104.1} -1 \right\}$

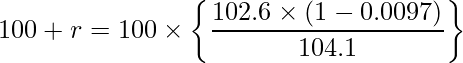
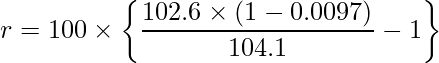
となります。

問3 [7]

問題文から式を立てると次のようになります。

$\displaystyle 102.6 \times \left\{\frac{100+r}{100} \right\}^3 = 105.6$

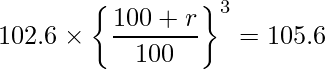
この式を展開すると、

$\displaystyle \left( \frac{100+r}{100} \right)^3 = \frac{105.6}{102.6}$

$\displaystyle \frac{100+r}{100} = \left( \frac{105.6}{102.6} \right)^\frac{1}{3}$

$\displaystyle 100+r= 100 \left( \frac{105.6}{102.6} \right)^\frac{1}{3}$

$\displaystyle r= 100 \left\{ \left( \frac{105.6}{102.6} \right)^\frac{1}{3} -1 \right\}$

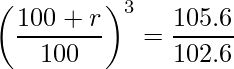
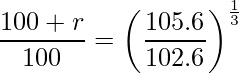
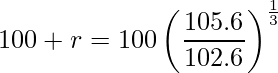
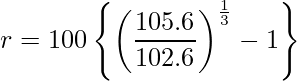
となります。

問4 [8]

I：×
「傾向変動」とは、時系列データにおける周期変動のうち、長期にわたる持続的な変化のことです。常に直線で表されるものではありません。

II：○
「季節変動」とは、時系列データにおける周期変動のうち、12ヶ月間で繰り返す周期変動のことです。

III：×
「不規則変動」とは、時系列データにおける周期変動のうち、傾向変動、循環変動、季節変動以外の変動のことです。不規則変動には、観測誤差など諸要因による変化が含まれます。

問5 [9]

「コレログラム」とは、「元のデータ」と「元のデータから時間をずらしたデータ」との相関係数を計算し、元データからずらした量（ラグ）を横軸に、計算した相関係数を縦軸に取ったグラフのことです。詳しくは「32-4. 自己相関」をご覧ください。

元のデータを見てみると、1年（12ヶ月）ごとの周期が見られます。したがって、ラグが「12」の倍数のところで自己相関係数が高くなり、ラグが「6」、「18」…のところで自己相関係数が低くなることが予想されます。したがって、正しいコレログラムは②となります。

問6 [10]

I：単純無作為抽出法
「単純無作為抽出法」とは、母集団から完全に、ランダムに標本を抽出する方法です。

II：層化抽出法
「層化抽出法」とは、母集団をその特性に応じていくつかの層に分類することが可能な場合に、各層からランダムに標本を抽出する方法のことです。出発便の時間が「層」に当たります。

III：集落抽出法
「集落抽出法」とは、母集団をいくつかのグループに分け、その中から無作為抽出で選ばれたグループに含まれる標本を全て抽出する方法のことです。クラスター抽出法とよばれる場合もあります。

ブログ