次のグラフは、新宿御苑における2015年8/1～8/3まで3日間の毎時気温データを表したものです。

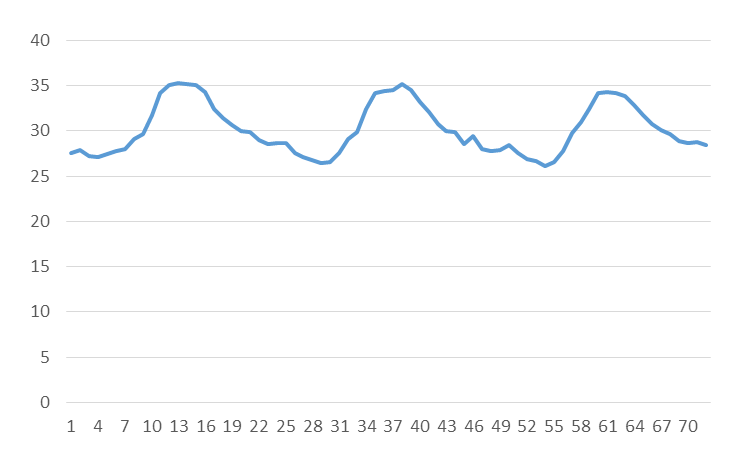
このグラフを見ると、同じような形が3回繰り返されていることが分かります。1日のうち昼は気温が高くなり夜は気温が下がるので、気温の変化の傾向は似通っており、ある程度の周期性が見て取れます。

ここで、「元のデータ」と「元のデータから時間をずらしたデータ」との相関係数を計算します。そして、元データからずらした量（ラグ）を横軸にとり、計算した相関係数を縦軸に取ると、次のようなグラフができます。

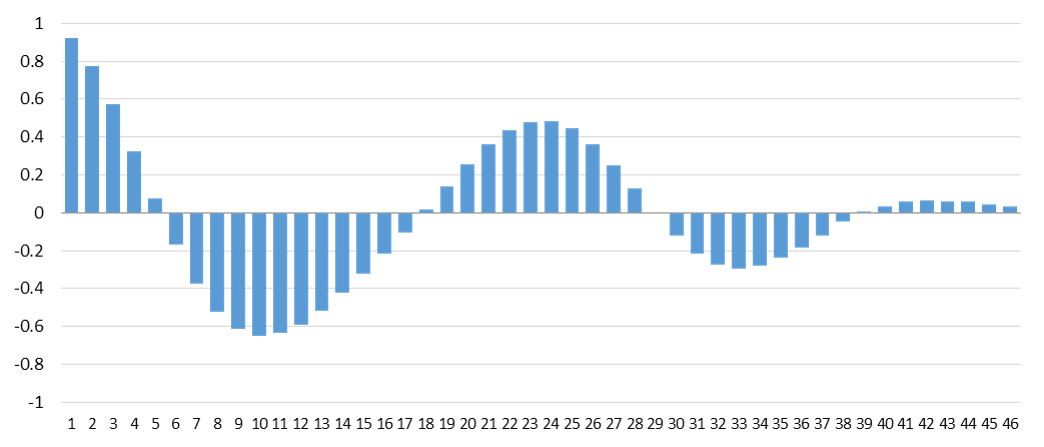
元データと時間をずらしたデータとの相関のことを「自己相関」と言います。また、ラグと自己相関を表したグラフを「コレログラム」と言います。コレログラムを見ると、データが周期性をもつかどうかを調べることができます。

このグラフの自己相関係は、コサインカーブが減衰していくような規則正しい形を描いています。データが「24」、「48」ずれたところで自己相関が極端に高くなっており、「12」、「36」で自己相関が極端に低くなっています。したがって、このデータは「24」の周期をもっており、似たような形を繰り返していることが推測できます。