- Step1. 基礎編
- 32. その他
32-2. 正規性の確認
データが正規分布に従うことを仮定する統計手法（母平均の推定など）を使う場合は、次のような方法を用いてデータの正規性を確認する必要があります。
- ヒストグラムを描く
- Q-Qプロットを描く
- 正規性の検定を行う
■ヒストグラムを描く
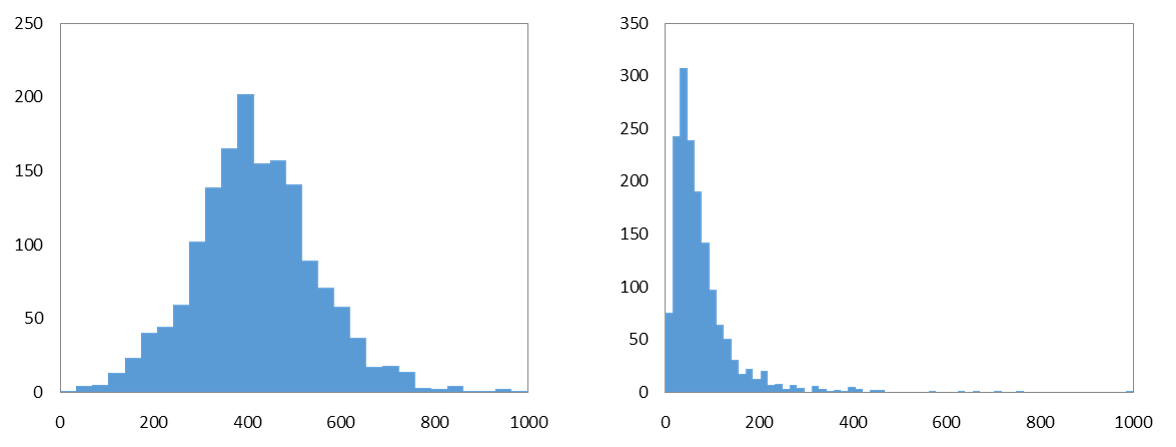
左のグラフでは平均値を中心に左右対称の山型の分布が見られることから、データは正規分布に従うと考えられます。一方の右のグラフでは分布が左に偏っており、右裾を引くヒストグラムであることから正規分布に従うとは言えません。
■Q-Qプロットを描く
Q-Qプロット（Quantile-Quantile Plot）は、2つの確率分布を比較するための図です。2つの分布が類似している場合には、プロットが一直線に並びます。
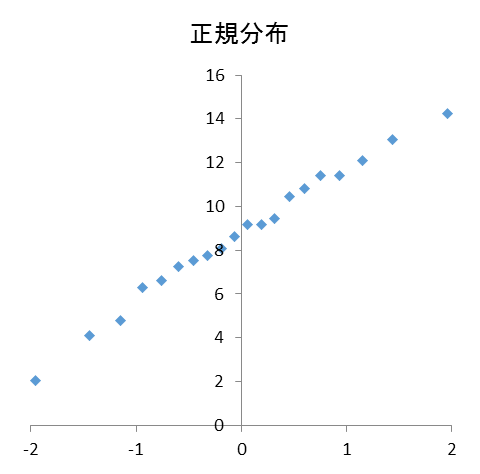
データが正規分布しているかを判断するための図を特に正規Q-Qプロットといいます。正規Q-Qプロットの縦軸は「データの値」を、横軸は「データの期待値を標準化した値（正規分布の理論値）」を表します。次の図で示すようにプロットが一直線に並ぶ場合、データは正規分布していると考えることができます。
正規Q-Qプロットは次の手順で作成します。
- データを小さい順に並べたものを準備する（
, 
, 
, 
, 
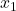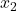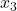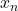） - 正規分布の累積分布関数を準備する
- 1と2のデータからそれぞれ分位数を取得する（
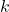/(データの数)%点の値 {: 
, 
, 
, , 
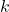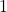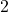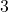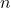}を取得する） - 1のデータから取得した分位数を縦軸に、2のデータから取得した分位数を横軸に取り、3で取得した値をプロットする
次のグラフは、様々なデータから作成した正規Q-Qプロットです。
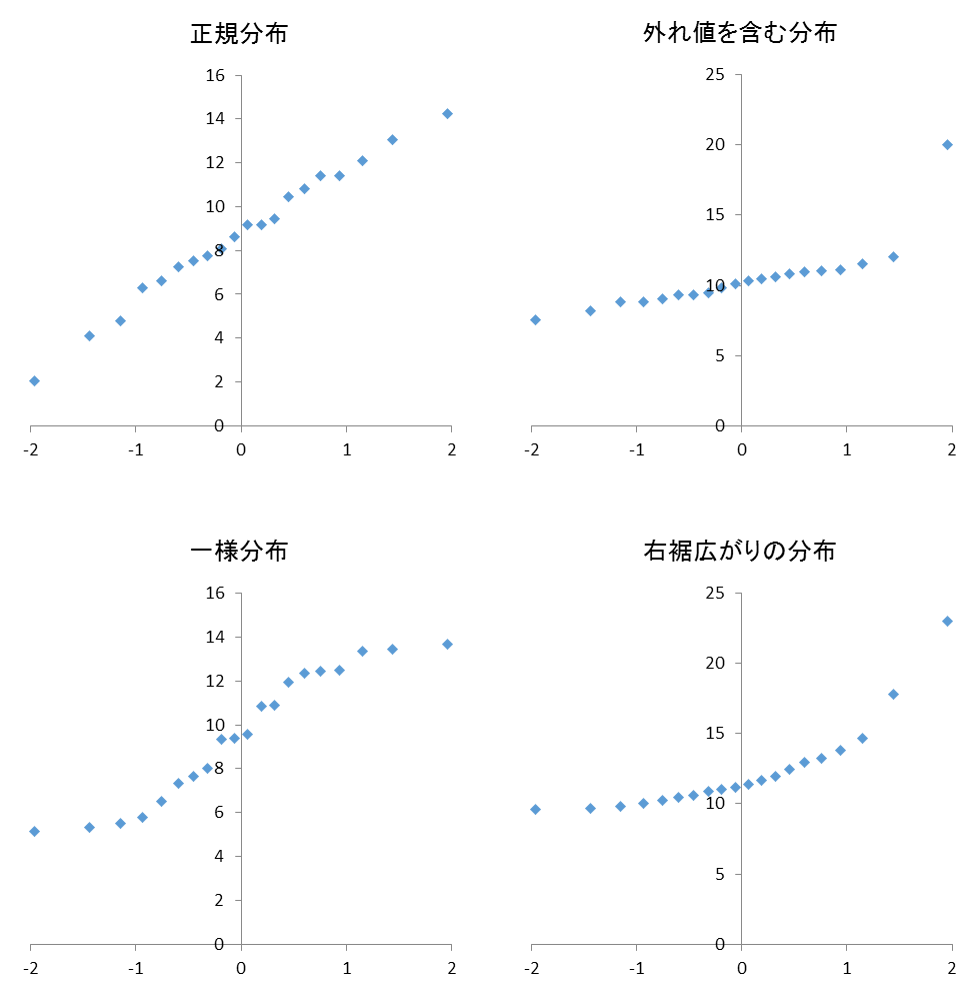
■正規性の検定を行う
正規性の検定には次に示すようにいろいろな検定方法があります。
- 歪度によるダゴスティーノ検定
- 尖度によるダゴスティーノ検定
- 歪度と尖度によるオムニバス検定
- コルモゴロフ=スミルノフ検定
- シャピロ=ウィルク検定
