正規確率プロットと正規性の検定・度数分布とヒストグラム─エクセル統計による解析事例
2017/04/19
カテゴリ：解析事例
※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。
分析データ
下図は、女子大生123人の身長を測定した結果（架空のデータ）です。ここでは、エクセル統計を用いて正規確率プロットの作成、正規性の検定、ヒストグラムの作成、適合度の検定を行うことでデータの正規性を調べます。
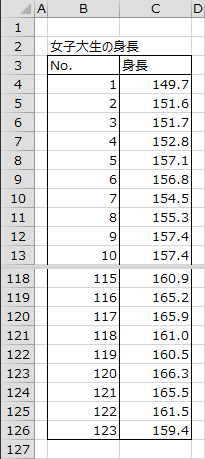
正規確率プロットと正規性の検定
まず、正規性の検定の有意水準を「0.05」に設定します。
続いて、セル「C3」を選択後、メニューより［エクセル統計］→［基本統計・相関］→［正規確率プロットと正規性の検定］を選択します。
ダイアログが表示される際、セル範囲「C3:C126」が［データ入力範囲］に自動で指定されます。このまま［OK］を選択して分析を実行します。
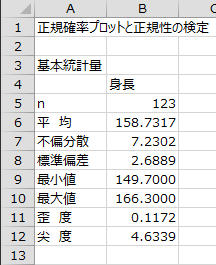
基本統計量
サンプルサイズ、平均、不偏分散、標準偏差、最小値、最大値、歪度、尖度が出力されます。データが正規分布している場合、歪度は0、尖度は3となりますが、尖度が4.6339なので正規分布よりも尖った分布となっています。
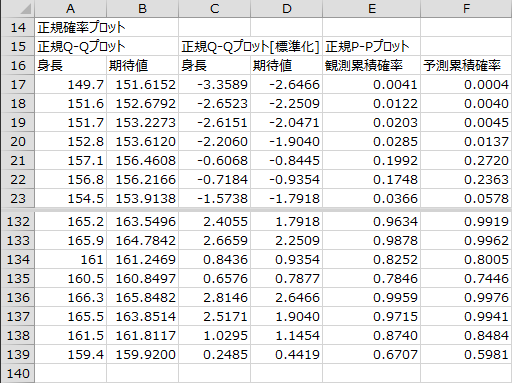
正規確率プロット（データ）
観測値による正規Q-Qプロットのためのデータ、観測値を標準化した値による正規Q-Qプロットのためのデータ、正規P-Pプロットのためのデータが出力されます。
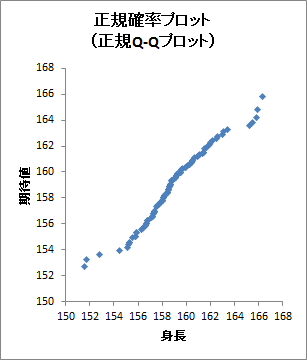
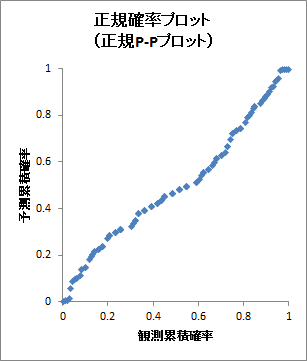
正規確率プロット（グラフ）
正規Q-Qプロット、正規Q-Qプロット［標準化］、正規P-Pプロットが出力されます。正規確率プロットは、プロットが直線状に分布していればデータが正規分布していることを表します。
正規性の検定
正規性の検定として、歪度によるダゴスティーノ検定、尖度によるダゴスティーノ検定、歪度と尖度によるオムニバス検定、コルモゴロフ=スミルノフ検定、シャピロ=ウィルク検定の結果が出力されます。
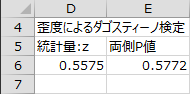
歪度によるダゴスティーノ検定の両側P値は0.5772なので帰無仮説は棄却されませんでした。尖度によるダゴスティーノ検定の両側P値は0.05未満なので帰無仮説は棄却されました。歪度は正規分布に近いですが、尖度は正規分布と離れていることを裏付けています。
帰無仮説：歪度 = 0
帰無仮説：尖度 = 3
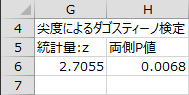
帰無仮説：母集団分布は正規分布である
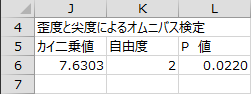
帰無仮説：母集団分布は正規分布である
帰無仮説：母集団分布は正規分布である
度数分布とヒストグラム
データの正規性を調べる場合、度数分布表から正規分布との適合度を検定したり、ヒストグラムを作成して分布の形状を確認したりする方法もあります。
先ほどと同様、セル「C3」を選択後、メニューより［エクセル統計］→［基本統計・相関］→［度数分布とヒストグラム］を選択します。
［階級設定］タブの［等間隔］オプションを選択し、［最小］と［間隔］を指定します。
［検定］タブでチェックボックス［適合度の検定（カイ二乗検定）を行う］にチェックを入れ、［OK］ボタンをクリックします。
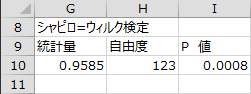
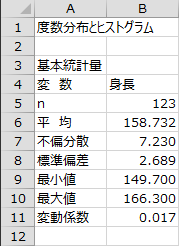
基本統計量
サンプルサイズ、平均、不偏分散、標準偏差、最小値、最大値、変動係数が出力されます。
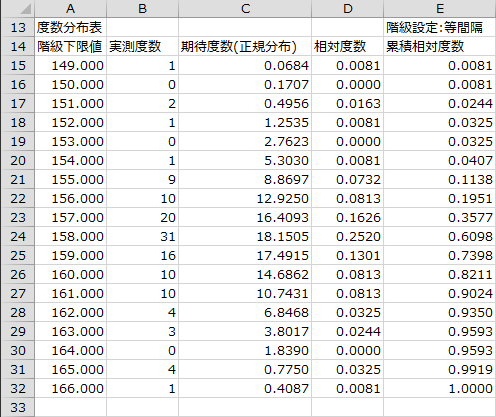
度数分布表
階級下限値、実測度数、（正規分布による）期待度数、相対度数、累積相対度数が出力されます。
適合度の検定
実測度数分布と期待度数分布について適合度の検定を行った結果が出力されます。P値が0.05未満なので、帰無仮説「母集団分布は正規分布である」は棄却されました。
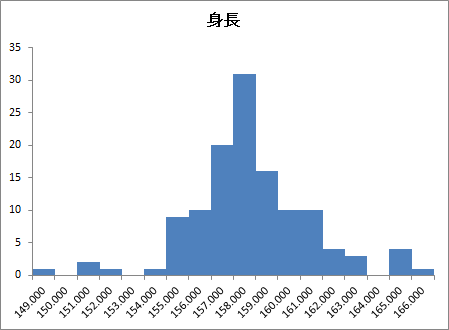
ヒストグラム
実測度数分布を元にヒストグラムが出力されます。
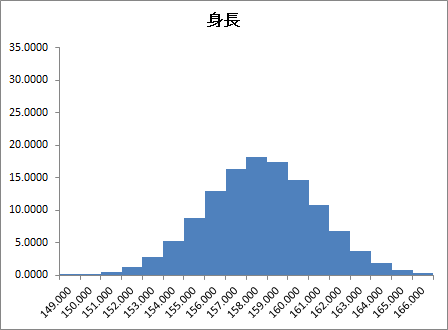
エクセル統計では出力されませんが、期待度数分布についてヒストグラムを作成すると下図のようになります。実測度数のヒストグラムよりもなだらかな山になっていることが確認できます。
考察
正規性の検定や適合度の検定の結果、ヒストグラムの形状から、今回のデータは正規分布していないと言えそうです。
※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。
ダウンロード
この解析事例のExcel ファイルのダウンロードはこちらから → example_16.xlsx
このファイルは、エクセル統計の体験版に対応しています。
