Cox比例ハザードモデル─エクセル統計による解析事例

2017/04/19

※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。

分析データ

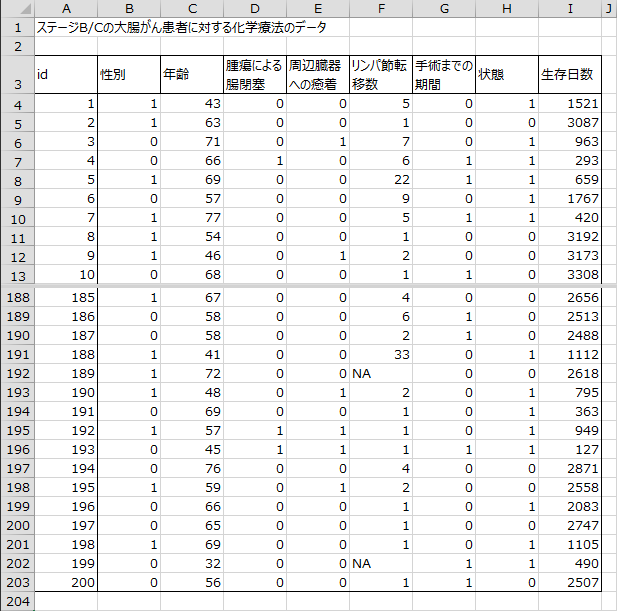
下図は、ステージB/Cの大腸がん患者に対する化学療法の生存時間のデータです。929人分のデータから上位200人分の死亡症例データを抜粋しています。状態データは、0を打ち切り、1を死亡としています。エクセル統計を用いてCox比例ハザードモデルを用いた生存時間解析を行い、共変量の与える影響を調べます。（出典：Laurie （1989））

ダイアログの設定

下図のように表の先頭行「B3:I3」を選択します。メニューより［エクセル統計］→［生存分析・ハザード分析］→［Cox比例ハザードモデル］を選択します。

［変数］タブ

ダイアログが表示される際、セル範囲「B3:I203」が［データ入力範囲］に自動で指定されます。「生存時間」を［時間］に、「状態」を［状態］に、その他の変数をすべて［共変量］に設定します。

［変数選択］タブ

［変数選択］タブで「方法」を［増減法］に設定し、［変数選択の過程を出力する］をオンにします。

［グラフ］タブ

［グラフ］タブで［生存率のグラフを出力する］、［モデル診断のためのlog-log生存率のグラフを出力する］、［曲線上の打ち切り例をマークで表示する］を選択します。

［オプション］タブ

［オプション］タブですべての項目を選択し、［OK］をクリックします。

出力内容

出力内容の目次がハイパーリンク付きで出力されます。

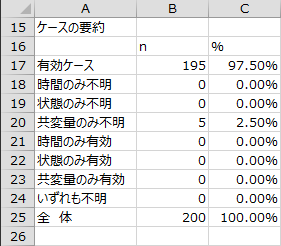
ケースの要約

「有効ケース」、「時間のみ不明」、「状態のみ不明」、「共変量のみ不明」、「時間のみ有効」、「状態のみ有効」、「共変量のみ有効」、「いずれも不明」、「全体」の件数および割合が出力されます。「有効ケース」が分析対象となります。

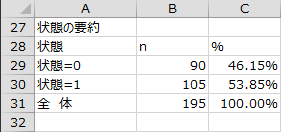
状態の要約

状態が「0」、「1」、「全体」の件数および割合が出力されます。

基本統計量

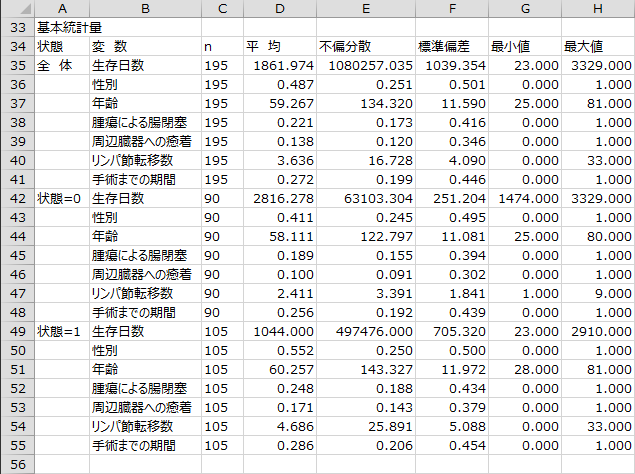
状態ごとの各変数の件数、平均、不偏分散、標準偏差、最小値、最大値が出力されます。

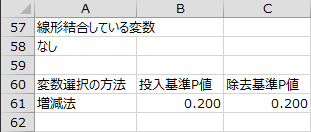
線形結合している変数・変数選択の方法

線形結合している変数の有無と変数選択の設定内容が出力されます。

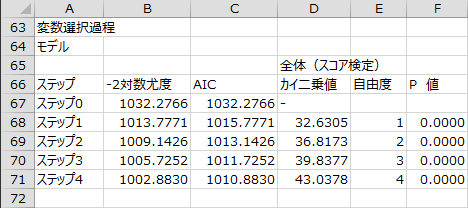
変数選択過程 - モデル

変数選択の各ステップで回帰式の精度を表す指標と変数選択により投入または除去された共変量が出力されます。

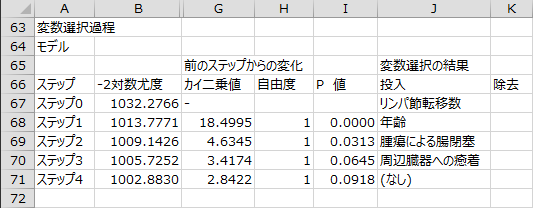
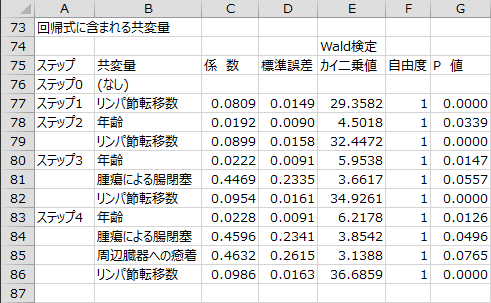
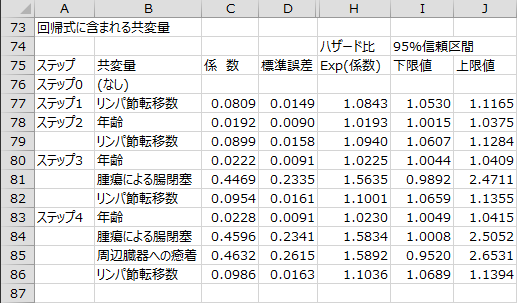
変数選択過程 - 回帰式に含まれる共変量

変数選択の各ステップで回帰式に含まれる共変量の偏回帰係数、偏回帰係数の標準誤差、偏回帰係数の有意性の検定の結果、ハザード比、ハザード比の95%信頼区間が出力されます。ステップ4で選択された共変量のP値がすべて基準値0.2を下回ったため、この時点で変数選択過程は終了となっています。

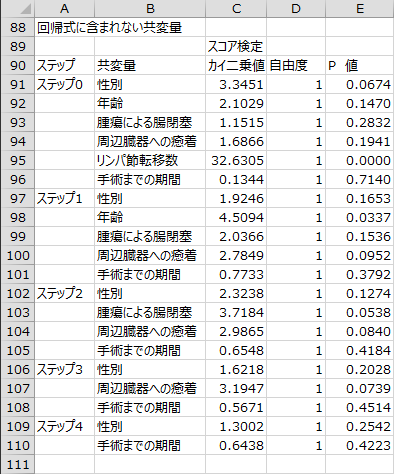
変数選択過程 - 回帰式に含まれない共変量

変数選択の各ステップで、回帰式に含まれない変数を回帰式に投入した場合の有意性をスコア統計量（カイ二乗値）を用いて検定した結果が出力されます。

各ステップで最もP値が小さい共変量を次のステップで投入します。ステップ0で最もP値が小さかった共変量である「リンパ節転移数」が、ステップ1で投入されています。

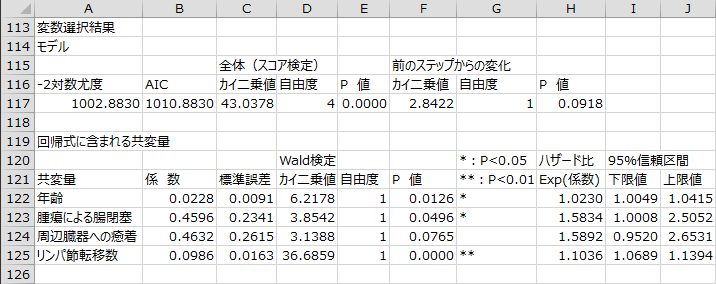
変数選択結果

変数選択の最後のステップにおける回帰式の精度と有意性、回帰式に含まれる共変量が出力されます。

変数選択の結果、「性別」と「手術までの期間」は回帰式に投入されませんでした。モデルのスコア検定のP値が0.01未満となり、5%有意水準でモデルに有意性が認められる結果となりました。

シミュレーション

各共変量の任意の値を罫線内に入力することで、推定した係数に基づくハザード比が出力されます。値A、値Bに値を入力した場合、予測値が「生存率」、「1-生存率」、「累積ハザード」、「log-log生存率」のグラフに反映されます。また、群1、群2に値を入力した場合、予測値が「モデル診断のためのlog-log生存率」のグラフに反映されます。

初期設定では値Aと群1には各共変量の最小値が、値Bと群2には各共変量の最大値が指定されています。

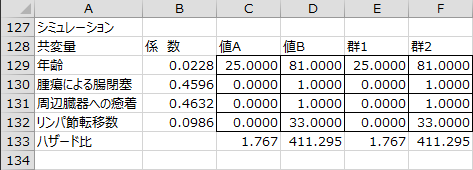
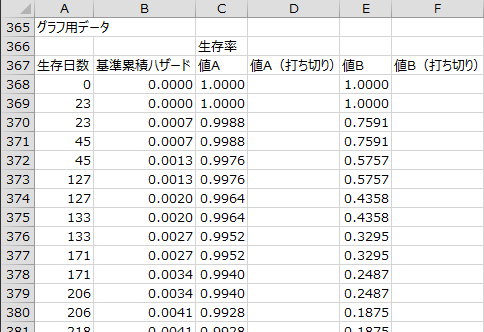
生存率曲線

推定した偏回帰係数とシミュレーションでの「値A」と「値B」の値に基づいた生存率曲線が出力されます。エクセル統計では、タイデータがある場合の基準累積ハザードの計算方法として、Breslowの近似法を用いています。

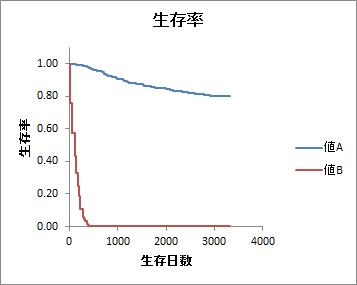
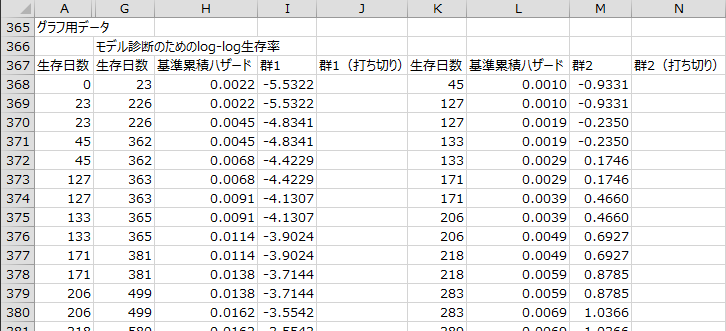
モデル診断のためのlog-log生存率

ハザード比の中央値でデータ全体を2群に分割し、各群でlog-log生存率を求めています。

このlog-log生存率曲線は、Cox比例ハザードモデルの比例ハザード性を確認するために用います。

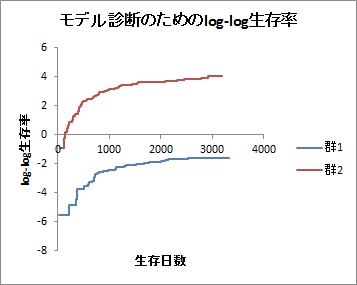
ケースごとの統計量

各生存時間における「基準生存率」、「基準累積ハザード」、「生存率」、「累積ハザード」、「log-log生存率」が出力されます。エクセル統計では、Breslowの近似により基準生存率関数の算出を行っています。

グラフ用データ

生存率曲線、およびモデル診断のためのlog-log生存率曲線を作成するためのデータが出力されます。

考察

増減法による変数選択を行った結果、「年齢」、「腫瘍による腸閉塞」、「周辺臓器への癒着」、「リンパ節転移数」の4つの共変量を含むモデルが推定されました。一方、「性別」と「手術までの期間」はモデルからは除去されました。

「モデル診断のためのlog-log生存率」を見ると、2本の曲線が交わらずに互いに平行移動した位置関係にあるので、比例ハザード性を仮定できると考えられます。

推定された係数の値はすべて「正」であることから、「年齢」が高く、「腫瘍による腸閉塞」および「周辺臓器への癒着」があり、「リンパ節転移数」が多いほど生存率は低下すると考えられます。

ダウンロード

この解析事例のExcel ファイルのダウンロードはこちらから　→　example_37.xlsx

このファイルは、エクセル統計の体験版に対応しています。

ブログ