箱ひげ図─エクセル統計による解析事例
2017/04/19
カテゴリ：解析事例
※ このコンテンツは「エクセル統計（BellCurve for Excel）」を用いた解析事例です。
分析データ
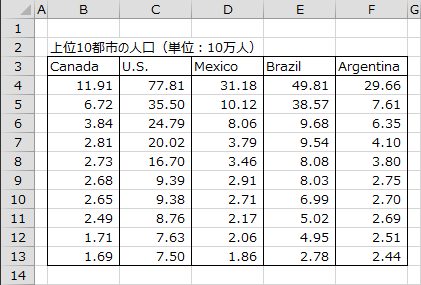
下図は、南北アメリカ大陸の5カ国について、ワールド年鑑（1967）を元に各国上位10都市の人口を調べた結果です（単位：10万人）。エクセル統計を用いて箱ひげ図を作成し、各国上位10都市の人口の分布の違いについて分析します。（David C. Hoaglin, Frederick Mosteller, John W. Tukey, "Understanding Robust and Exploratory Data Analysis", Wiley-Interscience, 2000, P66-67. 参照）
ダイアログの設定
下図のように、セル範囲「B3:F3」を選択後、メニューより［エクセル統計］→［基本統計・相関］→［箱ひげ図］を選択します。
ダイアログが表示される際、セル範囲「B3:F13」が［データ入力範囲］に自動で指定されます。［1 : Cutoff─Fourth─Med─Fourth─Cutoff］をクリックし、［OK］を選択して分析を実行します。
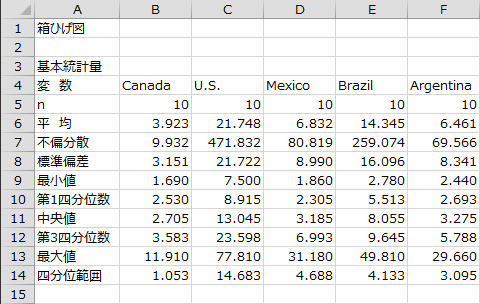
基本統計量
各列のサンプルサイズ、平均、不偏分散、標準偏差、最小値、第1四分位数、中央値、第3四分位数、最大値、四分位範囲が出力されます。
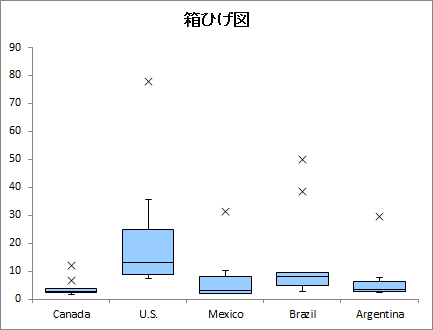
箱ひげ図
Tukey法による箱ひげ図が出力されます。Excel のグラフで縦棒と誤差範囲を用いて作成しています。
Tukey法
Tukey法による箱ひげ図の各点の計算方法について解説します。
中央値は以下のように定義されます。nはサンプルサイズ、kは正の整数、x(k) はデータ内でk番目に大きい値を表します。
fourthの（最小値または最大値からの）深さは以下のように定義されます。depth of median は中央値の深さ、［x］はxを超えない最大の整数を表します。mを正の整数とすると、fourthの深さがm+0.5となった場合、fourthの値はx(m) とx(m+1) の平均値となります。
理論上のcutoff は以下のように定義されます。fourth-spread は、上側のfourthと下側のfourthとの差です。実際の上側cutoff は、理論値以下で最大のデータとなります。また、実際の下側cutoff は、理論値以上で最小のデータとなります。
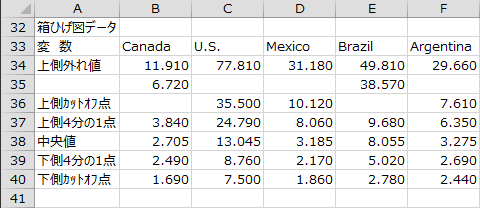
箱ひげ図データ
箱ひげ図の各点の値が出力されます。
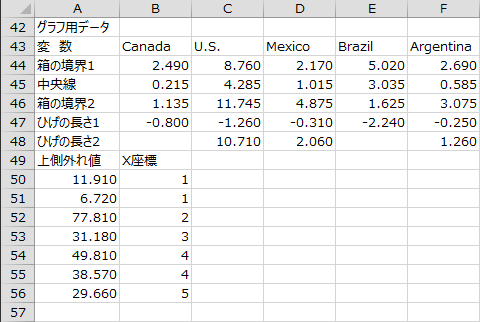
グラフ用データ
箱ひげ図のグラフの元データが出力されます。
※ 掲載している画像は、エクセル統計による出力後に一部書式設定を行ったものです。
ダウンロード
この解析事例のExcel ファイルのダウンロードはこちらから → example_29.xlsx
このファイルは、エクセル統計の体験版に対応しています。
