- Step1. 基礎編
- 3. さまざまな代表値
3-5. 歪度と尖度
■歪度(わいど)
分布が正規分布からどれだけ歪んでいるかを表す統計量で、左右対称性を示す指標のことです。サンプルサイズをn、各データ![]() の平均値を
の平均値を![]() 、標準偏差をsとすると歪度は次の式から求められます。
、標準偏差をsとすると歪度は次の式から求められます。
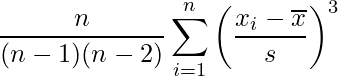
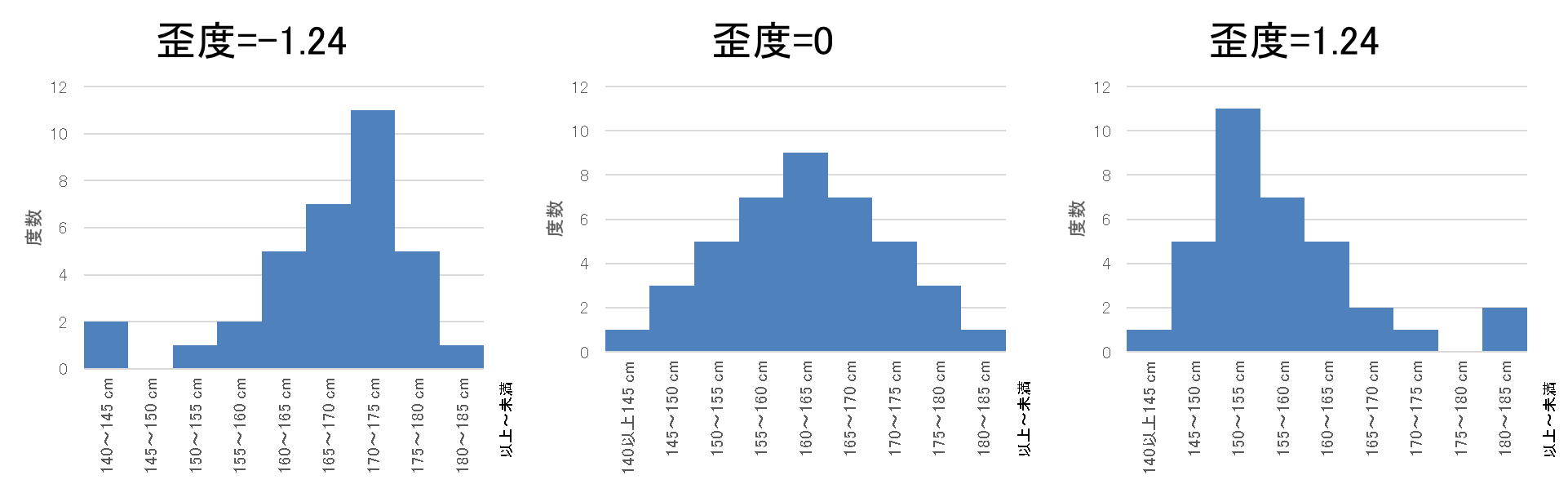
「右裾が長い」もしくは「右に歪んだ」もしくは「左に偏った」分布のときには正の値を、「左裾が長い」もしくは「左に歪んだ」もしくは「右に偏った」分布のときには負の値をとります。左右対称の分布(例えば正規分布)の場合には0になります。
例えば、3-2章で用いた生徒の身長のデータから歪度を算出すると次のようになります(※この図に示した歪度は、すべてのデータが階級値をとった場合の値です)。
■尖度(せんど)
分布が正規分布からどれだけ尖っているかを表す統計量で、山の尖り度と裾の広がり度を示します。サンプルサイズをn、各データ![]() の平均値を
の平均値を![]() 、標準偏差をsとすると尖度は次の式から求められます。
、標準偏差をsとすると尖度は次の式から求められます。
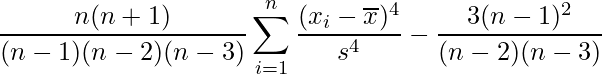
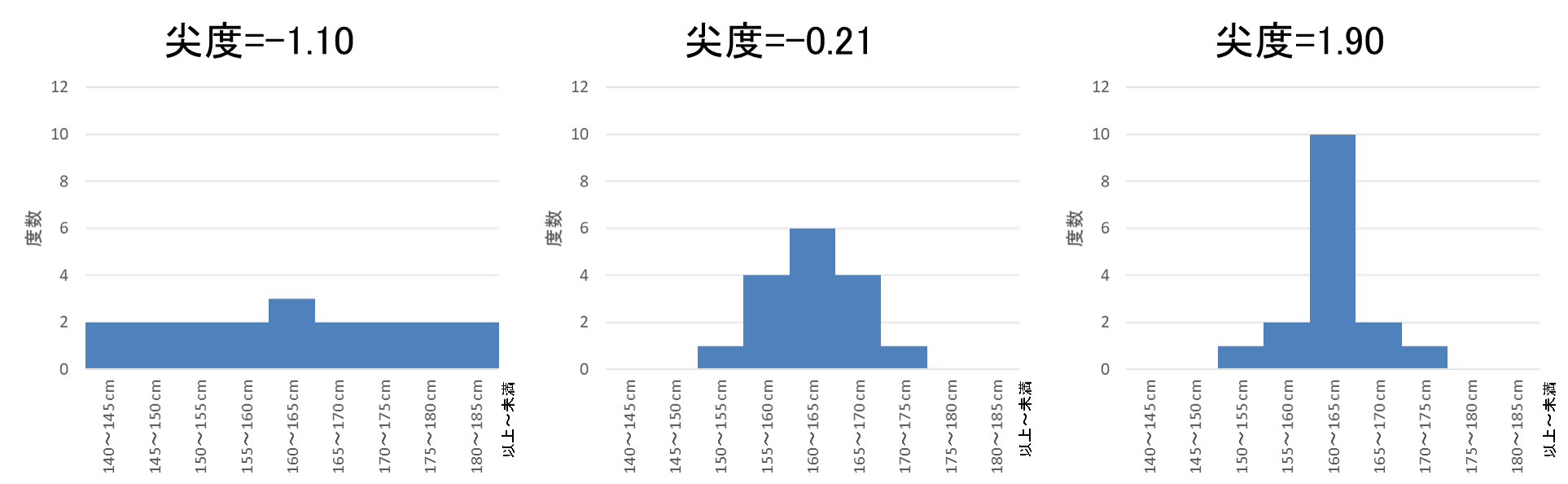
正規分布より尖った分布(データが平均付近に集中し、分布の裾が重い)のときには正の値を、正規分布より扁平な分布(データが平均付近から散らばり、分布の裾が軽い)のときには負の値をとります。正規分布の場合には0になります。
例えば、3-2章で用いた生徒の身長のデータ(一部改変)から尖度を算出すると次のようになります(※この図に示した尖度は、すべてのデータが階級値をとった場合の値です)。
尖度には2つの定義があります。この章で説明した「0を基準とする」定義のほか、「3を基準とする」定義があります(詳しくはこちら)。