- 3. さまざまな代表値
練習問題(3. さまざまな代表値)
1
次の表はあるクラス36人の100点満点の数学のテストの結果を度数分布表にしたものである。この度数分布表からクラスのおよその平均点を求めよ。
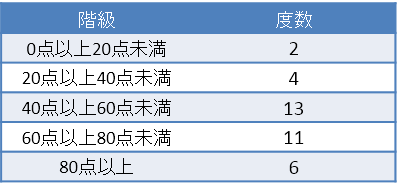

答えを見る
- 答え
 閉じる
閉じる -
度数分布表から平均値を求めるためには、「階級値」を使います。
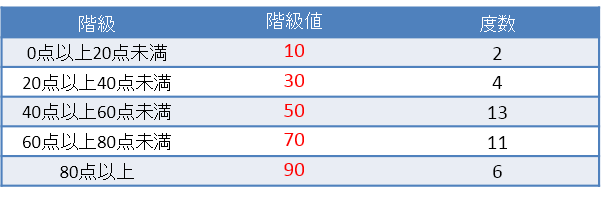
したがって、平均値は次のようになります。
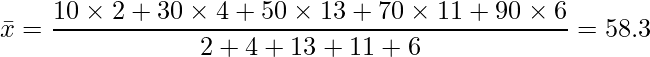
2
次の表はあるクラス50人の100点満点の国語のテストの結果をまとめたものである。この結果からクラスの平均点、中央値、モードを求めよ。
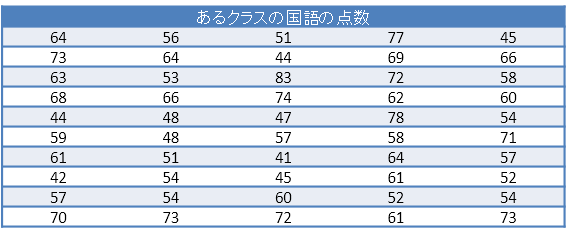

答えを見る
- 答え
 閉じる
閉じる -
■平均値
平均点は50人全ての国語のテストの点数を足して、50で割ることで算出できます。
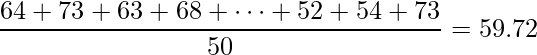
■中央値
中央値は、データの数が偶数のときは、真ん中に最も近い2つの値の平均値です。まずデータを小さい順に並べます。
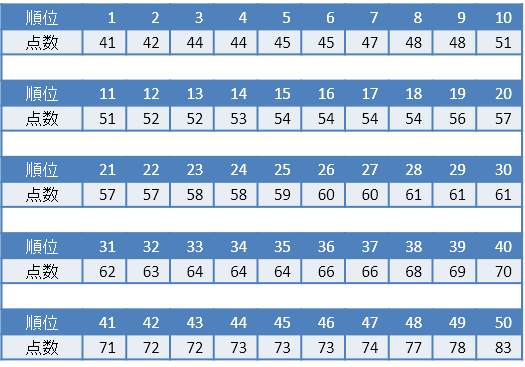
このクラスは偶数なので、ちょうど真ん中に位置する最も近い25番目の値「59」と26番目の値「60」の平均値が中央値となります。
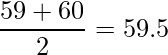
■モード
最も多い点数がモードとなります。このデータでは、「54点」がモードになります。
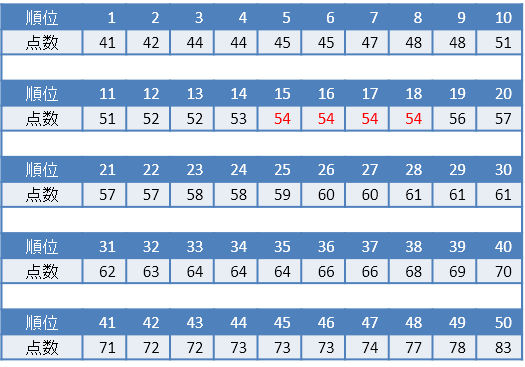
3
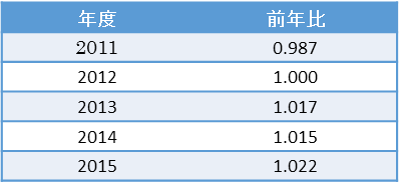
次の表は、2011年から2015年までの日本の年間GDPの前年比である。 このデータを用いて、5年間のGDPの平均成長率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
平均成長率は比率であるので、単純な算術平均ではなく幾何平均によって求める必要があります。この計算は、関数電卓もしくはExcelを用いて行うことができます。
![Rendered by QuickLaTeX.com \displaystyle\sqrt[5]{0.987 \times 1.000 \times 1.017 \times 1.015 \times 1.022} \fallingdotseq 1.008](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-fa1a26392dd8f05340caa86f224383ec_l3.png)
4
ある100kmの道を、はじめの20kmは時速50kmで、次の50kmは時速40kmで、最後の30kmは時速60kmで走った。この時の平均時速を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
平均時速は(距離)÷(かかった時間)で計算できるので、まず3つそれぞれの距離でかかった時間を算出します。
- 20kmの道:20÷50=0.4時間
- 50kmの道:50÷40=1.25時間
- 30kmの道:30÷60=0.5時間
したがって合計で0.4+1.25+0.5=2.15時間走ったことが分かります。この時間で、100kmの道を走ったことから、
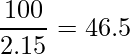
となり、答えは時速46.5kmとなります。
調和平均の算出式を使う場合には次のように計算します。この場合、走った距離が時速ごとに異なるので距離で重みを付けた調和平均(加重調和平均)として求めます。
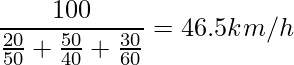
5
午前と午後でそれぞれ3000匹ずつのひよこを鑑定するノルマを課された 、一人のひよこ鑑定士について考える。ある日、午前中には1時間当たり1200匹のペースで鑑定し、午後は1時間当たり800匹のペースで鑑定した。
このひよこ鑑定士は、1日で平均すると一時間に何匹のペースでひよこを鑑定したことになるか。

答えを見る
- 答え
 閉じる
閉じる -
算術平均でも調和平均でも、どちらの方法を用いても計算することができます。
■算術平均
(ひよこを鑑定した数)÷(かかった時間)で計算できるので、まず午前中と午後にかかった時間を算出します。
- 午前中:3000÷1200=2.5時間
- 午後:3000÷800=3.75時間
となることから、合計で2.5+3.75=6.25時間仕事をしたことが分かります。この時間内で、併せて6000匹のひよこを鑑定したことから、
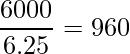
となり、答えは960匹/時間となります。
■調和平均
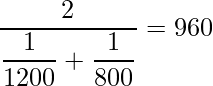
と計算できます。







