- Step1. 基礎編
- 3. さまざまな代表値
3-3. 平均・中央値・モードの使い方
次のヒストグラムはランダムに選んだ社会人36人に貯蓄額をインタビューした結果です。
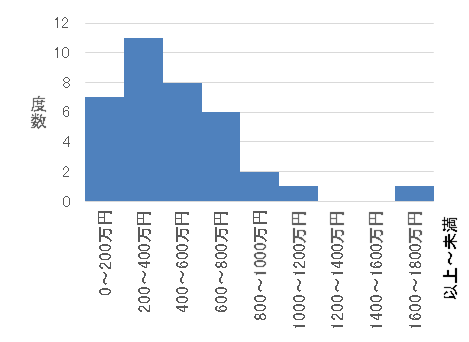
36人の貯蓄額の平均は「475万円」でした。「結構多いな」と思われるかもしれません。これは、貯蓄額が1700万円という飛び抜けて大きな額の人が1人いたために、平均が大きくなってしまっているのです。このように、非常に大きい値や非常に小さい値を少数含むデータの場合、平均が引きづられてしまうためにデータの特徴を掴みきれない場合があります。
このような場合には、中央値を見るとデータの傾向を別の面から捉えることができます。このデータの場合、中央値は「400万円」でした。つまり、ちょうど真ん中くらいの生活水準の人の貯蓄額は「400万円」程度であることが分かります。
また、モードを使うと「ボリュームゾーン」とよばれる最も頻度の高い層が分かります。このデータでは、モードは「200~400万円」の階級で、度数は11です。したがって36人のうち約3分の1の人がこの層に属しているということが分かります。
【コラム】ヒストグラムの山が2個ある場合
ヒストグラムを描くと、分布の山が2つ以上現れる場合があります。例えば次のヒストグラムでは分布の山が2つできています。このようなデータを「多峰性 (multimodal)」といい、特に分布の山が2つのものを「二峰性 (bimodal)」といいます。一方、分布の山が1つのものを「単峰性 (unimodal)」といいます。
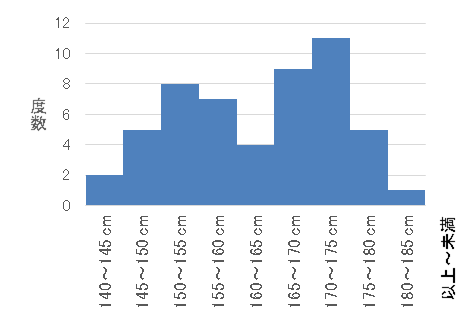
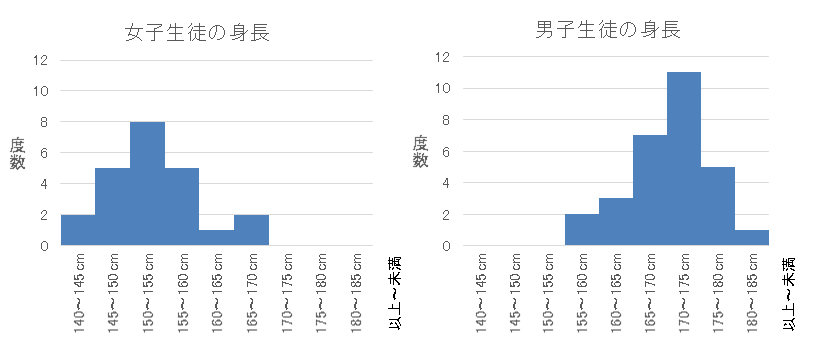
二峰性のデータの場合、異なる性質の集団が混ざっている可能性があります。このデータの場合、男子生徒と女子生徒という2つの集団が混ざっているために分布の山が2つになっています。このような場合、集団を性質によって2つに分けてヒストグラムを作ると、分かりやすくなります。
■おすすめ書籍
なんと1968年に出版された本ですが、今でも十分に統計学の勉強になります。
3. さまざまな代表値
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 3. さまざまな代表値
3-1. 平均・中央値・モード
- 3. さまざまな代表値
3-2. 平均・中央値・モードの関係
- ブログ
平均値と統計法







