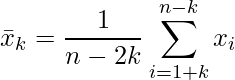一般的な平均、つまりデータの値を全て足してデータの数で割ったもの、は「算術平均」と呼ばれます。平均にはこの算術平均以外に「幾何平均」や「調和平均」といったものがあります。

■幾何平均

幾何平均は次の式から求めます。

幾何平均は比率や割合で変化するものに対してその平均を求めるときに使います。例えば過去3年間で家賃が20％、10％、15％上昇したときに、1年で平均何％上昇したかを算出する際に用いられます。

この時の平均は幾何平均の式に当てはめて次のように求められます。（この計算は一般的な電卓ではできませんので関数電卓もしくはExcelで行ってください。）

■調和平均

調和平均は時速の平均などを求めるときに使います。調和平均は次の式から求めます。

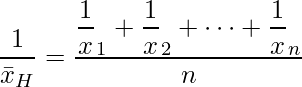
この式を変形すると次の式になります。

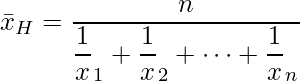
例えば、行き時速60km、帰り時速80kmでドライブをした時の平均時速を算出する際に用いられます。この時の平均は調和平均の式に当てはめて次のように求められます。

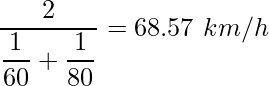
■刈込み平均 (トリム平均)

データを小さい順に並べたとき、小さい側と大きい側からそれぞれ指定した個数の値を除き、残ったデータのみから求める平均のことです。例えば、大小k個ずつのデータを除いた刈込み平均は次の式から求めます。