※コラム「統計備忘録」の記事一覧はこちら※

Excelの分析ツールを使った重回帰分析で、結果が出てこなくて不便に思うものに標準偏回帰係数があります。英語ではstandardized partial regression coefficientですから、標準化偏回帰係数としたほうが良いかもしれませんね。統計ソフトで重回帰分析を行えば必ず出力されます（エクセル統計も勿論出力します）。

Excel分析ツールの出力結果（標準偏回帰係数の出力は無い）

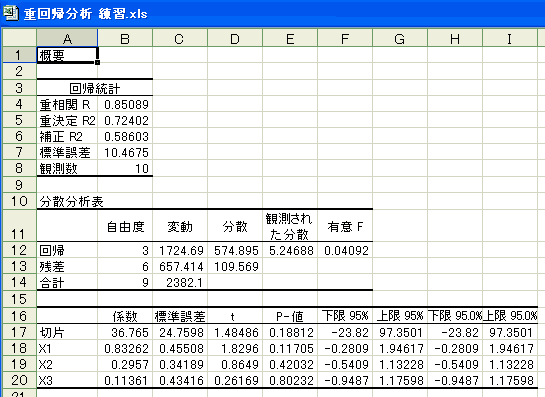
Excelで標準偏回帰係数を計算したいのなら2つの方法が考えられます。1番目の方法は、全部の変数の値をｚ得点に変換してから重回帰分析を行います。こうすると、偏回帰係数（下図の係数の箇所）の値は標準偏回帰係数に一致します。

z得点に変換して重回帰分析をした結果

2番目は、偏回帰係数、説明変数の標準偏差、目的変数の標準偏差を使って計算します。計算式は次のとおりです。

標準偏回帰係数＝偏回帰係数×説明変数の標準偏差÷目的変数の標準偏差

さて、偏回帰係数と標準偏回帰係数の違いについて見てみましょう。偏回帰係数の大きさは説明変数と目的変数の関係性より、各変数の標準偏差の大きさや単位に影響を受けます。どういうことかは、次の2つのグラフを見比べてください。2つのグラフはデータの散らばりも回帰直線の傾きもそっくりに見えます。しかし、よく見ると回帰係数（説明変数が1つの時は単に回帰係数と言います）も座標軸の目盛も全く異なります。

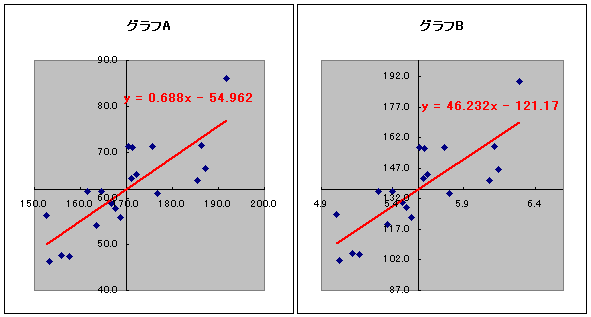
種を明かすと、どちらも同じ20人の身長と体重を測定したものですが、左のグラフAがセンチメートルとキログラム、右のグラフBがフィートとポンドによる結果です。単位を変えてしまったことで、身長と体重の関係性は同じでも回帰係数は大きく異なってしまいました。

次のグラフCは身長、体重ともにをz 得点に変換したものです。X軸もY軸も1目盛が1標準偏差に相当します。回帰直線の回帰係数を見ると0.807になっていますね。この0.807が標準回帰係数です。

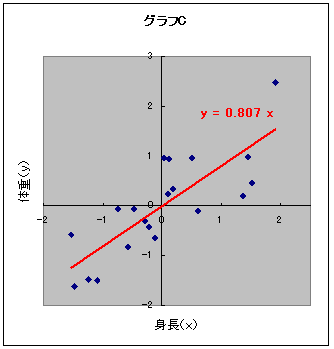
標準（偏）回帰係数は、説明変数の1標準偏差あたりの増減が、目的変数の1標準偏差あたりにどの程度影響しているかを示しています。例えば、身長以外に腹部の皮下脂肪の厚さを説明変数に加えたとしたら、身長と皮下脂肪のどちらが体重への影響が大きいかは、偏回帰係数を比べるよりも標準偏回帰係数を比べた方が適切です（ダイエット効果を評価するためなら偏回帰係数しか要りませんが）。

説明変数間の比較をするだけなら、説明変数だけ標準化すれば事足りますが、目的変数も標準化することで標準偏回帰係数の値は、ほとんどが1から-1の間に入ります。この間に値が収まらないときは多重共線性を疑ってみるとよいでしょう。