統計検定2級CBT公式問題集の解説(標本分布の分野)
2023/09/16
カテゴリ:統計検定
※統計検定2級 解説記事一覧はこちら※
下記のリンクからそれぞれの問題の解説に飛ぶことができます。
- 問1:標本割合
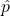 の標本分布に関する問題
の標本分布に関する問題 - 問2:標本分布の中央値等に関する問題
- 問3:推定量の分散に関する問題
- 問4:和と差の確率変数の性質に関する問題
- 問5:t分布の確率計算に関する問題
- 問6:分散・共分散・相関係数に関する問題
- 問7:
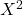 の期待値に関する問題
の期待値に関する問題 - 問8:F分布の特徴付けに関する問題
問1
![]() を標準化するには、
を標準化するには、![]() から
から ![]() を引いたものを
を引いたものを ![]() で割ります。標準化した式を用いて95%信頼区間を求めると、
で割ります。標準化した式を用いて95%信頼区間を求めると、
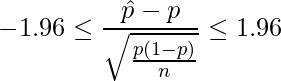
となります。変形すると、
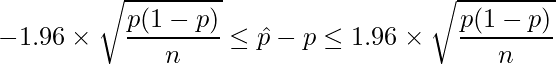
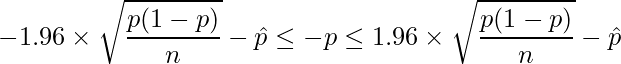
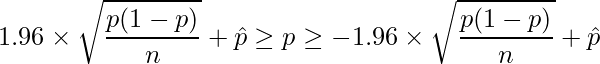
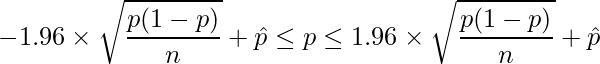
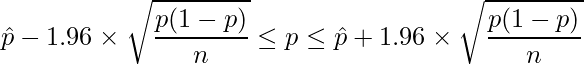
となります。
標本比率を用いた母比率の信頼区間算出の詳細については「21-1. 母比率の信頼区間の求め方1」をご覧ください。
問2
母集団{2, 4, 6, 8}から大きさ2の標本を無作為復元抽出する場合のすべてのパターンは次のようになります。復元抽出なので、1回目に抽出した値(左側の値)と2回めに抽出した値(右側の値)を区別する必要があるところがポイントです。
- (2, 2), (2, 4), (2, 6), (2, 8)
- (4, 2), (4, 4), (4, 6), (4, 8)
- (6, 2), (6, 4), (6, 6), (6, 8)
- (8, 2), (8, 4), (8, 6), (8, 8)
それぞれのパターンにおける標本平均 ![]() は次のようになります。
は次のようになります。
- (2, 2)=2, (2, 4)=3, (2, 6)=4, (2, 8)=5
- (4, 2)=3, (4, 4)=4, (4, 6)=5, (4, 8)=6
- (6, 2)=4, (6, 4)=5, (6, 6)=6, (6, 8)=7
- (8, 2)=5, (8, 4)=6, (8, 6)=7, (8, 8)=8
標本平均 ![]() の値と頻度を整理すると
の値と頻度を整理すると
| 標本平均 | パターン | 頻度 |
|---|---|---|
| 2 | (2, 2) | 1 |
| 3 | (2, 4), (4, 2) | 2 |
| 4 | (2, 6), (4, 4), (6, 2) | 3 |
| 5 | (2, 8), (4, 6), (6, 4), (8, 2) | 4 |
| 6 | (4, 8), (6, 6), (8, 4) | 3 |
| 7 | (6, 8), (8, 6) | 2 |
| 8 | (8, 8) | 1 |
となります。この表から、中央値、最頻値ともに5であることが分かります。
問3
問題文より ![]() と
と ![]() の差を2で割ることでBの重さを推定することができます。
の差を2で割ることでBの重さを推定することができます。
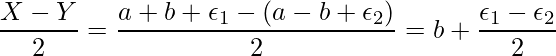
コインBの重さの重さの推定量は ![]() であり、その誤差は
であり、その誤差は![]() です。問題文より、
です。問題文より、![]() と
と ![]() の分布は独立であることから、コインBの重さの重さの推定量の分散は
の分布は独立であることから、コインBの重さの重さの推定量の分散は
![Rendered by QuickLaTeX.com \displaystyle V \left[ \frac{X-Y}{2} \right] = V \left[ \frac{X}{2} \right] + V \left[ \frac{Y}{2} \right] = \frac{\sigma^2}{4} + \frac{\sigma^2}{4} = \frac{\sigma^2}{2}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-4e4cd349f892367c211fa903ef8cce1a_l3.png)
となります。
2変数の分散については「15-6. 2変数の期待値と分散」をご覧ください。
問4
![]() と
と ![]() の平均を計算してみます。
の平均を計算してみます。
次に、![]() と
と ![]() の分散を計算してみます。
の分散を計算してみます。![]() と
と ![]() は互いに独立であることから、
は互いに独立であることから、
となります。最後に、![]() と
と ![]() の共分散を計算してみます。
の共分散を計算してみます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle Cov(U, V) &=& E[(U-E[U])(V-E[V])] \\ &=& E[((X+Y)-E[X+Y])((X-Y)-E[X-Y])] \\ &=& E[(X+Y)(X-Y)-(X+Y)E[X-Y] \\ &-& E[X+Y](X-Y)+E[X+Y]E[X-Y])] \\ &=& E[(X+Y)(X-Y)] - E[X+Y]E[X-Y] \\ &-& E[X+Y]E[X-Y] + E[X+Y]E[X-Y] \\ &=& E[X^2-Y^2] - E[X+Y]E[X-Y] \\ &=& E[X^2] - E[Y^2] - (E[X] + E[Y])(E[X] - E[Y]) \\ &=& E[X^2] - E[Y^2] - ((E[X])^2 - (E[Y])^2) \\ &=& E[X^2] - (E[X])^2 - (E[Y^2] - (E[Y])^2 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-0ff05f53d3a47e60867ade932c9c8a9d_l3.png)
ここで分散の定義より
であることから、
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle Cov(U, V) &=& E[X^2] - (E[X])^2 - (E[Y^2] - (E[Y])^2 \\ &=& V[X] - V[Y] \\ &=& \sigma^2_1 - \sigma^2_2 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-590787450fb5e81b9fd5669b012c5c88_l3.png)
となります。
I:◯
![]() と
と ![]() の平均の計算結果より、正しいことがわかります。
の平均の計算結果より、正しいことがわかります。
II:◯
共分散 ![]() が0の場合、
が0の場合、![]() と
と ![]() は互いに独立であるといえます。
は互いに独立であるといえます。![]() と
と ![]() の共分散の計算結果より、
の共分散の計算結果より、![]() となります。この値が0になるのは
となります。この値が0になるのは ![]() の場合です。
の場合です。
III:◯
![]() と
と ![]() の平均と分散の計算結果より、どちらも平均が0、分散が
の平均と分散の計算結果より、どちらも平均が0、分散が ![]() の正規分布に従います。
の正規分布に従います。
問5
母平均を ![]() 、標本平均を
、標本平均を ![]() 、標本から算出した不偏分散を
、標本から算出した不偏分散を ![]() 、サンプルサイズを
、サンプルサイズを ![]() とすると、次に示す統計量
とすると、次に示す統計量 ![]() の値は、自由度
の値は、自由度 ![]() の t分布に従います。
の t分布に従います。
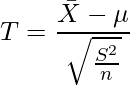
したがって、問題文で与えられた ![]() は自由度
は自由度 ![]() の
の ![]() 分布に従います。ここで、
分布に従います。ここで、
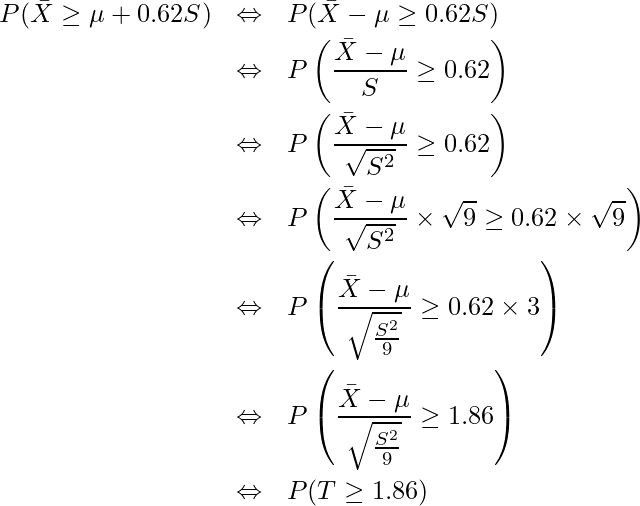
と変形できます。t分布表から自由度8の行を見ると、上側確率が ![]() となる点が
となる点が ![]() であることがわかります。すなわち、
であることがわかります。すなわち、
となる確率は0.05となります。
t分布の詳細については「20-1. 標本とt分布」をご覧ください。
問6
問題文より、確率変数 ![]() 、
、![]() 、
、![]() はいずれも標準化されていることから、
はいずれも標準化されていることから、
となります。また、確率変数 ![]() と
と ![]() の相関係数
の相関係数 ![]() は次の式から算出できます。
は次の式から算出できます。
![Rendered by QuickLaTeX.com \displaystyle r = \frac{Cov(X,Y)}{\sqrt{V[X]V[Y]}}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-01ce339949d0f1e18aeb6f6203c365e1_l3.png)
![]() と
と ![]() との相関係数は0.5であることから
との相関係数は0.5であることから
![Rendered by QuickLaTeX.com \displaystyle \frac{Cov(X_1,X_2)}{\sqrt{V[X_1]V[X_2]}} = \frac{Cov(X_1,X_2)}{\sqrt{1 \times 1}} = Cov(X_1,X_2) = 0.5](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-534b281e84e84f476f1dd3d431d68f42_l3.png)
となります。同様に計算すると、
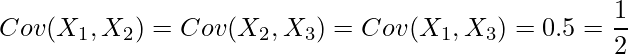
となります。![]() と
と ![]() との相関係数は
との相関係数は
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle r &=& \frac{Cov(X_1,Y)}{\sqrt{V[X_1]V[Y]}} \\ &=& \frac{Cov \left( X_1,\frac{X_1 + X_2 + X_3}{3} \right) }{\sqrt{1 \times V \left[\frac{X_1 + X_2 + X_3}{3} \right]}} \\ &=& \frac{\frac{Cov(X_1,X_1) + Cov(X_1,X_2) + Cov(X_1,X_3)}{3} }{\sqrt{V \left[ \frac{X_1 + X_2 + X_3}{3} \right]}} \\ &=& \frac{\frac{1}{3} Cov(X_1, X_1) + \frac{1}{3} Cov(X_1, X_2) + \frac{1}{3} Cov(X_1, X_3) }{A} \\ &=& \frac{\frac{1}{3} Cov(X_1, X_1) + \frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{2} }{\sqrt{\frac{1}{9} \times \left(1 + 1 + 1 + 2 \times \frac{1}{2} + 2 \times \frac{1}{2} + 2 \times \frac{1}{2} \right)}} \\ &=& \frac{\frac{1}{3} Cov(X_1, X_1) + \frac{2}{6}}{\sqrt{\frac{6}{9}}} \\ &=& \frac{\frac{1}{3} Cov(X_1, X_1) + \frac{1}{3}}{\sqrt{\frac{2}{3}}} \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-eb0eb9223f7d3238cea403e69ec8bf80_l3.png)
ただし、![]() である。ここで
である。ここで ![]() と
と ![]() の相関係数が1であることを利用すると、
の相関係数が1であることを利用すると、
![Rendered by QuickLaTeX.com \displaystyle \frac{Cov(X_1,X_1)}{\sqrt{V[X_1]V[X_1]}} = \frac{Cov(X_1,X_1)}{\sqrt{1 \times 1}} = Cov(X_1,X_1) = 1](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-325c1e02492f740994e2562eaf672773_l3.png)
となることから、上の式に代入すると
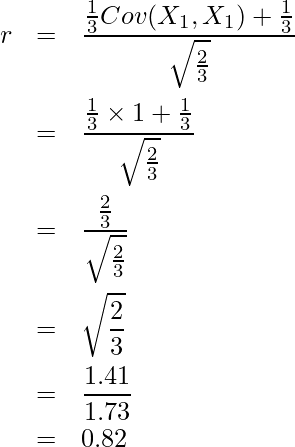
となります。
共分散の詳細については「15-6. 2変数の期待値と分散」をご覧ください。
問7
問題文より
となります。分散は次のように計算することができます。
この式を利用すると、
となります。
確率変数の分散の詳細については「12-5. 確率変数の分散」をご覧ください。
問8
さまざまな確率分布の定義をまとめてみます。
- カイ二乗分布
- t分布
- F分布
![]() ,
, ![]() , …,
, …, ![]() が互いに独立で標準正規分布
が互いに独立で標準正規分布 ![]() に従う確率変数であるとき、次の式から算出される
に従う確率変数であるとき、次の式から算出される![]() は自由度
は自由度 ![]() のカイ二乗分布に従います。
のカイ二乗分布に従います。
自由度が1のとき、カイ二乗分布は標準正規分布に従う確率変数を二乗したものに等しくなります。
標準正規分布 ![]() に従う
に従う ![]() と自由度
と自由度 ![]() のカイ二乗分布
のカイ二乗分布 ![]() があり、これらが互いに独立であるとき、次の式から算出される
があり、これらが互いに独立であるとき、次の式から算出される ![]() は自由度
は自由度 ![]() のt分布に従います。
のt分布に従います。
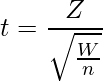
F分布は、自由度が ![]() 、
、![]() のカイ二乗分布
のカイ二乗分布 ![]() 、
、![]() が互いに独立である場合に、次の式から算出されるFが従う確率分布のことです。このときFは自由度
が互いに独立である場合に、次の式から算出されるFが従う確率分布のことです。このときFは自由度 ![]() のF分布に従います。
のF分布に従います。
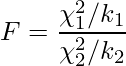
これらの定義を問題文で与えられた数式に照らし合わせてみます。定義より、![]() は自由度5のカイ二乗分布に従います。また、
は自由度5のカイ二乗分布に従います。また、![]() は自由度5のt分布に従います。
は自由度5のt分布に従います。![]() は次のように書き換えることができます。
は次のように書き換えることができます。
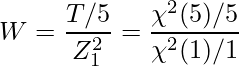
この式から、![]() は自由度(5, 1)のF分布に従うことが分かります。
は自由度(5, 1)のF分布に従うことが分かります。
次に ![]() を計算します。
を計算します。![]() は自由度5のt分布に従うことから、
は自由度5のt分布に従うことから、![]() の値を計算するためには、t分布表の自由度5の行から上側2.5%点となる値が必要です(|V|となっているので、上側と下側合わせて0.05 (5%) となる確率を計算します)。t分布表を見ると「2.571」となっているので、
の値を計算するためには、t分布表の自由度5の行から上側2.5%点となる値が必要です(|V|となっているので、上側と下側合わせて0.05 (5%) となる確率を計算します)。t分布表を見ると「2.571」となっているので、
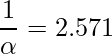
となることから、これを解いて ![]() となります。
となります。
カイ二乗分布の詳細については「22-1. カイ二乗分布」を、t分布の詳細については「20-1. 標本とt分布」を、F分布の詳細については「28-1. F分布」をご覧ください。







