下記のリンクからそれぞれの問題の解説に飛ぶことができます。

• 問1：二項分布に関する問題
• 問2：確率分布の再現性に関する問題
• 問3：二項分布に従う確率変数の分布に関する問題
• 問4：確率分布のパラメータに関する問題
• 問5：二項分布の計算に関する問題
• 問6：ポアソン分布の計算に関する問題

問1

【ア】【イ】二項分布の定義についてです。「コインを投げたときに表が出るか裏が出るか」のように、何かを行ったときに起こる結果が2つしかない試行のことを「ベルヌーイ試行」といいます。このベルヌーイ試行を複数回行ったときに、成功する回数が従う確率分布を「二項分布」といいます。詳しくは「13-1. 二項分布」をご覧ください。

【ウ】【エ】【オ】二項分布のパラメータは「試行回数n」と「成功の確率α」の2つです。これらのパラメータを使うと、確率変数Xの期待値はE(X)=nα、分散はV(X)=nα(1-α)となります。詳しくは「13-2. 二項分布の期待値と分散」をご覧ください。

【カ】確率分布の再生性とは、同じ確率分布を持つ2つの独立な確率変数の和は同じ確率分布を持つことです。

【キ】【ク】【ケ】ポアソン分布は二項分布から考えることができます。すなわち、試行回数nが十分大きく、成功確率αが非常に小さい場合、「nα=一定」と考えることができます。そこでを「nα=β」とおくと、成功回数は「ポアソン分布」に従うと考えることができます。詳しくは「13-3. ポアソン分布」をご覧ください。確率変数Xがポアソン分布に従っている時、Xの期待値と分散はともにE(X)=V(X)=βとなります。

問2

再生性を持つ確率分布として、二項分布、ポアソン分布、正規分布などがあげられます。正規分布の再生性については「14-2. 正規分布の再生性と標準正規分布」をご覧ください。

問3

すでにn=8、α=0.2のときの値があたえられているので、すべての値を逆転させることでn=8、α=0.8のときの分布を描くことができます。例えば、P(X=8)=0.17、P(X=7)=0.34…となります。

真面目に計算すると、

…となります。

問4

代表的な確率分布とパラメータの数を以下に記載します。

• 正規分布：2個
• 二項分布：2個
• ポアソン分布：1個
• 幾何分布：1個
• 超幾何分布：3個
• ガンマ分布：2個
• 指数分布：1個
• t分布：1個
• カイ二乗分布：1個
• F分布：2個

問5

この問題は二項分布を使って計算できます。試行回数n=8、雨が降る確率α=10/30=1/3（去年の天候より）、雨が降らない確率1-α=2/3なので、求める確率は次のように計算できます。

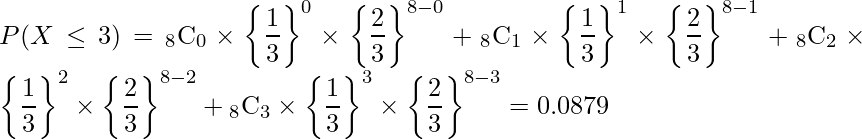
問6

この問題は二項分布を使って計算できますが、生起確率が非常に小さいことからポアソン分布を使って計算できます。試行回数n=50、生起確率α=3/1000を用いて、β=nα=50×3/1000=0.15となります。

この値を用いて、求める確率は次のように計算できます。